题目内容
6. 一个面积为100cm2的矩形,被分成9个小矩形,现知四个小矩形面积为A=4cm2,B=14cm2,C=3cm2,D=6cm2,求矩形E的面积.
一个面积为100cm2的矩形,被分成9个小矩形,现知四个小矩形面积为A=4cm2,B=14cm2,C=3cm2,D=6cm2,求矩形E的面积.
分析 图中的9个矩形是大矩形是被4条直线分割后得到的,矩形的面积等于一组邻边的乘积,从横向来看,两个相邻矩形的倍比关系是一致的,D是A的$\frac{3}{2}$倍,那么C也是②的$\frac{3}{2}$倍,从而求出②的面积,同理得到①、②的面积.由②、A、B的面积间的数量关系可以推知③、E、④间的数量关系.
解答  解:由题意知:D是A的$\frac{3}{2}$倍,那么C也是②的$\frac{3}{2}$倍,①也是B的$\frac{3}{2}$倍,
解:由题意知:D是A的$\frac{3}{2}$倍,那么C也是②的$\frac{3}{2}$倍,①也是B的$\frac{3}{2}$倍,
所以②的面积是:3×$\frac{2}{3}$=2(cm2),①的面积是:14×$\frac{3}{2}$=21(cm2),
∴S③:SE:S④=S②:SA:SB=2:4:14,
∴SE=$\frac{2}{10}$×(100-50)=10(cm2),
即矩形E的面积是10cm2.
点评 此题考查了矩形的性质.注意组合图形的面积的计算方法.

练习册系列答案
相关题目
16. 如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
 如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )| A. | 46° | B. | 44° | C. | 36° | D. | 22° |
11.已知二次函数y=ax2+bx+c与x的部分对应值如下表所示:
则下列对该函数的判断中正确的是( )
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -2 | 1 | 2 | 1 | … |
| A. | 图象开口向上 | B. | y的最小值为-2 | ||
| C. | 图象与y轴相交于负半轴 | D. | 方程ax2+bx+c=0的正根在2与3之间 |
15.查看表格,根据表中提供的信息确定k,b的值,并将表格填写完整:直线y=kx+b不经过哪几个象限?
| x | 0 | 1 | 2 |
| y=kx | 0 | 1 | 2 |
| y=kx+b | 1 | 2 | 3 |
16.分式$\frac{1}{a+1}+\frac{1}{a(a+1)}$的计算结果是( )
| A. | $\frac{1}{a+1}$ | B. | $\frac{a+1}{a}$ | C. | $\frac{a}{a+1}$ | D. | $\frac{1}{a}$ |
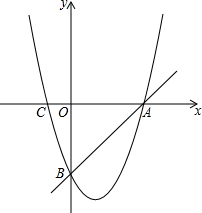 如图,抛物线y=x2-2x+n与直线y=x-3相交于A、B两点(点A在x轴上,点B在y轴上),与x轴的另一个交点为点C.
如图,抛物线y=x2-2x+n与直线y=x-3相交于A、B两点(点A在x轴上,点B在y轴上),与x轴的另一个交点为点C.