题目内容
4.一只口袋里放着4个红球、8个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀.(1)取出红球的概率为$\frac{1}{5}$,白球有多少个?
(2)取出黑球的概率是多少?
(3)再在原来的袋中放进多少个红球,能使取出红球的概率达到$\frac{1}{3}$?
分析 (1)首先设袋中有白球x个.由题意得:4+8+x=4×5,解此方程即可求得答案;
(2)由只口袋里放着4个红球、8个黑球和8个白球,这三种球除颜色外没有任何区别,直接利用概率公式求解即可求得答案;
(3)首先设再在原来的袋中放入y个红球.由题意得:3(4+y)=20+y,或2(4+y)=8+8,继而求得答案.
解答 解:(1)设袋中有白球x个.
由题意得:4+8+x=4×5,
解得:x=8,
答:白球有8个;
(2)取出黑球的概率为:$\frac{8}{4+8+8}=\frac{2}{5}$,
答:取出黑球的概率是$\frac{2}{5}$,
(3)设再在原来的袋中放入y个红球.
由题意得:3(4+y)=20+y,或2(4+y)=8+8,
解得:y=4,
答:再在原来的袋中放进4个红球,能使取出红球的概率达到$\frac{1}{3}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
15.(1)填表
(2)由上表你发现了什么规律(请你用语言叙述出来)?
(3)根据你发现的规律填空:
①已知$\root{3}{3}$≈1.442,则$\root{3}{3000}$≈14.42
②已知$\root{3}{0.000456}$≈0.07697,则$\root{3}{456}$≈7.697.
| a | 0.000008 | 0.008 | 8 | 8000 | 8000000 |
| $\root{3}{a}$ | 0.02 | 0.2 | 2 | 20 | 200 |
(3)根据你发现的规律填空:
①已知$\root{3}{3}$≈1.442,则$\root{3}{3000}$≈14.42
②已知$\root{3}{0.000456}$≈0.07697,则$\root{3}{456}$≈7.697.
19.下列事件是随机事件的是( )
| A. | 购买一张福利彩票,中奖 | |
| B. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| C. | 太阳每天从东边升起 | |
| D. | 在一个仅装着白球和黑球的袋中摸出红球 |
16. 如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
 如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )| A. | 46° | B. | 44° | C. | 36° | D. | 22° |
 如图所示,8个相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是300cm2.
如图所示,8个相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是300cm2.
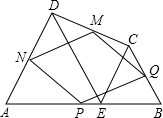 如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P、Q、M、N分别为AB、BC、CD、DA的中点,则四边形MNPQ是( )
如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P、Q、M、N分别为AB、BC、CD、DA的中点,则四边形MNPQ是( )