题目内容
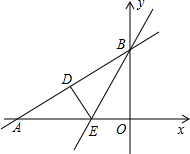 直角三角形AOB在平面直角坐标系中如图,O与坐标原点重合,点A在x轴上,点B在y轴上,OB=2
直角三角形AOB在平面直角坐标系中如图,O与坐标原点重合,点A在x轴上,点B在y轴上,OB=2| 3 |
(1)求直线BE的解析式;
(2)求点D的坐标;
(3)点M是直线BE上的动点,过M点作AB的平行线交y轴于点N,是否存在这样的点M,使得以点M、N、D、B为顶点的四边形是平行四边形?求出所有M点的坐标.
考点:一次函数综合题
专题:
分析:(1)在直角△OBE中求得E和B的坐标,然后利用待定系数法求得BE的解析式;
(2)过D作DG⊥OA于G,在直角△DGE中,利用三角函数即可求得DG和GE的长,则D的坐标即可求得;
(3)过D作DM1⊥y轴交BE于M,过M1作AB平行线交y轴于N1,和过D作DN2∥BE交y轴于N2,过N2作N2M2∥AB交直线EB于M2,两种情况进行讨论.
(2)过D作DG⊥OA于G,在直角△DGE中,利用三角函数即可求得DG和GE的长,则D的坐标即可求得;
(3)过D作DM1⊥y轴交BE于M,过M1作AB平行线交y轴于N1,和过D作DN2∥BE交y轴于N2,过N2作N2M2∥AB交直线EB于M2,两种情况进行讨论.
解答:解:(1)∵∠BAO=30°
∴∠ABO=60°,
∵沿BE折叠O.D重合
∴∠EBO=30°,
OE=
BE,
设OE=x,
则(2x)2=x2+(2
)2,
∴x=2,
即 BE=4,
E(-2,0),
设y=kx+b代入得;
解得
,
∴直线BE的解析式是:y=
x+2
,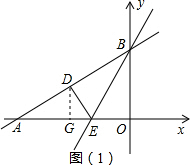
(2)过D作DG⊥OA于G,如图1(1),
∵沿BE折叠O、D重合,
∴DE=2,
∵∠DAE=30°
∴∠DEA=60°,∠ADE=∠BOE=90°,
∴∠EDG=30°,
∴GE=1,DG=
,
∴OG=1+2=3,
∴D的坐标是:D(-3,
);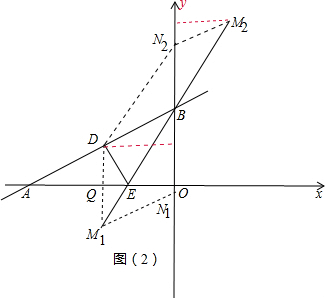
(3)存在,如图(2)
过D作DM1⊥y轴交BE于M,过M1作AB平行线交y轴于N1,
则M1的横坐标是x=-3,代入直线BE的解析式得:
y=-
,
∴M1(-3,-
),
②过D作DN2∥BE交y轴于N2,过N2作N2M2∥AB交直线EB于M2,
∵D的横坐标是-3,
∴M2的横坐标是3,
∵M1的坐标是(-3,-
),D(-3,
),
∴DM1=
+
=2
=NB,
∵BO=2
,
∴M2的纵坐标是2
+2
+
=5
,
∴M2(3,5
),
∴M点的坐标是:(-3,-
)和(3,5
).
∴∠ABO=60°,
∵沿BE折叠O.D重合
∴∠EBO=30°,
OE=
| 1 |
| 2 |
设OE=x,
则(2x)2=x2+(2
| 3 |
∴x=2,
即 BE=4,
E(-2,0),
设y=kx+b代入得;
|
解得
|
∴直线BE的解析式是:y=
| 3 |
| 3 |

(2)过D作DG⊥OA于G,如图1(1),
∵沿BE折叠O、D重合,
∴DE=2,
∵∠DAE=30°
∴∠DEA=60°,∠ADE=∠BOE=90°,
∴∠EDG=30°,
∴GE=1,DG=
| 3 |
∴OG=1+2=3,
∴D的坐标是:D(-3,
| 3 |

(3)存在,如图(2)
过D作DM1⊥y轴交BE于M,过M1作AB平行线交y轴于N1,
则M1的横坐标是x=-3,代入直线BE的解析式得:
y=-
| 3 |
∴M1(-3,-
| 3 |
②过D作DN2∥BE交y轴于N2,过N2作N2M2∥AB交直线EB于M2,
∵D的横坐标是-3,
∴M2的横坐标是3,
∵M1的坐标是(-3,-
| 3 |
| 3 |
∴DM1=
| 3 |
| 3 |
| 3 |
∵BO=2
| 3 |
∴M2的纵坐标是2
| 3 |
| 3 |
| 3 |
| 3 |
∴M2(3,5
| 3 |
∴M点的坐标是:(-3,-
| 3 |
| 3 |
点评:本题考查了一次函数的图象和性质,解此题的关键是用两点坐标用待定系数法求出解析式,再利用平行线间的距离处处相等求出点的横坐标.利用直角三角形的性质和勾股定理用方程求出点的纵坐标,注意一题多解.

练习册系列答案
相关题目
 在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).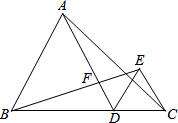 已知:如图,点D是线段BC上的任意一点,△ABD和△DCE都是等边三角形,AD与BE交于点F.
已知:如图,点D是线段BC上的任意一点,△ABD和△DCE都是等边三角形,AD与BE交于点F.