题目内容
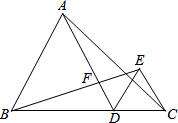已知：如图，点D是线段BC上的任意一点，△ABD和△DCE都是等边三角形，AD与BE交于点F．（1）求证：△BDE≌△ADC；
（2）求证：AB2=BC•AF；
（3）若BD=12，CD=6，求∠ABF的正弦值．
考点：相似三角形的判定与性质,全等三角形的判定与性质,等边三角形的性质,勾股定理
专题：
分析：（1）由△ABD和△DCE都是等边三角形，得出BD=AD，DE=DC，∠FAB=∠ABC=∠ADB=∠EDC，进而得出∠BDE=∠ADC，即可求证△BDE≌△ADC；
（2）由△FAB∽△ABC，得出
=
，即可得出AB2=BC•AF，
（3）由△FAB∽△ABC，得出∠ABF=∠ACB，可求sin∠ACB，即可得出∠ABF的正弦值．
（2）由△FAB∽△ABC，得出
| AF |
| AB |
| AB |
| BC |
（3）由△FAB∽△ABC，得出∠ABF=∠ACB，可求sin∠ACB，即可得出∠ABF的正弦值．
解答：证明：（1）∵△ABD和△DCE都是等边三角形
∴BD=AD，DE=DC，∠FAB=∠ABC=∠ADB=∠EDC=60°，
∴∠BDE=∠ADC．
在△BDE和△ADC中，
，
∴△BDE≌△ADC（SAS）；
（2）∵△BDE≌△ADC
∴∠DBE=∠DAC
∵∠ABC=∠ADB=60°
∴∠ABF=∠BCA
∵∠FAB=∠ABC，∠ABF=∠BCA，
∴△FAB∽△ABC，
∴
=
，
即AB2=BC•AF，
（3）如图，
∵△FAB∽△ABC
∴∠ABF=∠ACB，
过A作AM⊥BC于点M
∵△ABD是等边三角形，BD=12
∴MD=6，AM=6
，
在Rt△AMC中，AC=
=6
，
∴sin∠ACB=
=
=
，
即sin∠ABF=
．
∴BD=AD，DE=DC，∠FAB=∠ABC=∠ADB=∠EDC=60°，
∴∠BDE=∠ADC．
在△BDE和△ADC中，
|
∴△BDE≌△ADC（SAS）；
（2）∵△BDE≌△ADC
∴∠DBE=∠DAC
∵∠ABC=∠ADB=60°
∴∠ABF=∠BCA
∵∠FAB=∠ABC，∠ABF=∠BCA，
∴△FAB∽△ABC，
∴
| AF |
| AB |
| AB |
| BC |
即AB2=BC•AF，
（3）如图，
∵△FAB∽△ABC
∴∠ABF=∠ACB，
过A作AM⊥BC于点M
∵△ABD是等边三角形，BD=12
∴MD=6，AM=6
| 3 |
在Rt△AMC中，AC=
| AM2+MC2 |
(6
|
| 7 |
∴sin∠ACB=
| AM |
| AC |
6
| ||
6
|
| ||
| 7 |
即sin∠ABF=
| ||
| 7 |
点评：本题主要考查了相似三角形的判定与性质，全等三角形的判定与性质，等边三角形的性质及勾股定理，解题的关键是证出△FAB∽△ABC．
练习册系列答案
相关题目
已知，如图，A是圆O外一点，AO的延长线交圆O于点C，点B在圆上，且AB=BC，∠A=30°，求证：AB是圆O的切线．
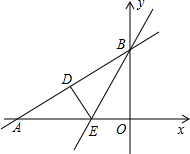直角三角形AOB在平面直角坐标系中如图，O与坐标原点重合，点A在x轴上，点B在y轴上，OB=2
为了了解某初中学生的体能情况，抽取若干名男学生在单位时间内进行引体向上测试，将所得数据（所有的数据为整数）整理后，画出频数分布直方图（如图），