题目内容
6．
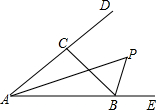如图，△ABC的角平分线AP和外角平分线BP相交于点P，求证：点P也在∠BCD的平分线上．
分析 作PF⊥AB于F，PG⊥BC于G，PH⊥AC于H，根据角平分线的性质定理和判定定理证明即可．
解答 证明：
作PF⊥AB于F，PG⊥BC于G，PH⊥AC于H，
∵BP是∠EBC的平分线，PF⊥AB，PG⊥BC，
∴PF=PG，
∵AP是∠BAC的平分线，PH⊥AC，PF⊥AB，
∴PH=PF，
∴PG=PH，PG⊥BC，PH⊥AC，
∴点P在∠BCD的平分线上．
点评 本题考查的是角平分线的性质和判定，掌握角的平分线上的点到角的两边的距离相等、到角的两边的距离相等的点在角的平分线上是解题的关键．
练习册系列答案
相关题目
16．若代数式$\frac{{\sqrt{x-1}}}{x-2}$有意义，则x必须满足的条件是（ ）
| A． | x＞1且x≠2 | B． | x＞1 | C． | x≠2 | D． | x≥1且x≠2 |
如图，在直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变换成△OA3B3，已知：A（1，3）、A1（2，3）、A2（4，3）、A3（8，3）、B（2，0）、B1（4，0）、B2（8，0）、B3（16，0）．求：
18．在式子$\sqrt{{x^2}+8}$中，则x的取值范围（ ）
| A． | x≥2$\sqrt{2}$ | B． | x≤2$\sqrt{2}$ | C． | x≥-2$\sqrt{2}$ | D． | 全体实数 |
如图所示，在象棋盘上建立平面直角坐标系，使使“马”位于点（2，2），“炮”位于点（-1，2），写出“兵”所在位置的坐标．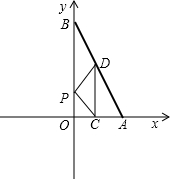
一次函数y=kx+b的图象与x，y轴分别交于点A（2，0），B（0，4）．