题目内容
11.观察下列一组数:-$\frac{1}{2}$,$\frac{2}{5}$,-$\frac{3}{10}$,$\frac{4}{17}$,-$\frac{5}{26}$…它们是按一定规律排列的,那么这组数的第10个数是$\frac{10}{101}$,第n个数为(-1)n$\frac{n}{{n}^{2}+1}$.分析 分子是从1开始连续的自然数,分母是分子的平方加1,奇数位置为负,偶数位置为正,由此得出第n个数为(-1)n$\frac{n}{{n}^{2}+1}$,利用规律得出答案即可.
解答 解:∵:-$\frac{1}{2}$,$\frac{2}{5}$,-$\frac{3}{10}$,$\frac{4}{17}$,-$\frac{5}{26}$…
∴第n个数为(-1)n$\frac{n}{{n}^{2}+1}$,
∴这组数的第10个数是$\frac{10}{101}$.
故答案为:$\frac{10}{101}$.,(-1)n$\frac{n}{{n}^{2}+1}$.
点评 此题考查数字的变化规律,找出数字的运算规律与符号排列的规律,利用规律解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.在绝对值小于100的整数中,可以写成整数平方的个数为( )
| A. | 18 | B. | 19 | C. | 10 | D. | 9 |
16.一个自然数的算术平方根是a,那么比这个数大2的自然数的算术平方根( )
| A. | a2+2 | B. | a+2 | C. | $\sqrt{a+2}$ | D. | $\sqrt{{a^2}+2}$ |
1.某同学在解方程3x-1=□x+1时,把□处的数字看错了,解得x=-2,则该同学把□看成了( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 4 | D. | $-\frac{1}{4}$ |
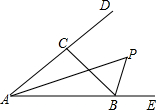 如图,△ABC的角平分线AP和外角平分线BP相交于点P,求证:点P也在∠BCD的平分线上.
如图,△ABC的角平分线AP和外角平分线BP相交于点P,求证:点P也在∠BCD的平分线上.