题目内容
20.若等腰三角形的一边长为6,另两边长分别是关于x的方程x2-(m+2)x+2m+4=0的两个根,则m=6或7.分析 先由关于x的方程x2-(m+2)x+2m+4=0有两个实数根,得出△=(m+2)2-4(2m+4)=m2-4m-12≥0,求出m的取值范围.再分类讨论:当6为等腰三角形的底边,则方程有等根,所以△=(m+2)2-4(2m+4)=0,解得m1=6,m2=-2(舍去);当6为等腰三角形的腰,则x=6为方程的解,把x=6代入方程可计算出m的值.
解答 解:∵关于x的方程x2-(m+2)x+2m+4=0有两个实数根,
∴△=(m+2)2-4(2m+4)=m2+4m+4-8m-16=m2-4m-12≥0,
∴m≥6或m≤-2.
当6为等腰三角形的底边,根据题意得△=(m+2)2-4(2m+4)=0,解得m1=6,m2=-2,
当m=-2时,根据根与系数的关系得两腰的和=m+2=0,不合题意舍去;
当6为等腰三角形的腰,则x=6为方程的解,把x=6代入方程得36-6(m+2)+2m+4=0,解得m=7.
故答案为6或7.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.也考查了根的判别式,一元二次方程的解的定义,等腰三角形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下面是某同学在一次测验中解答的填空题:①若x2=a2,则x=a;②方程2x(x-1)=x-1的解为x=$\frac{1}{2}$;③若分式$\frac{{x}^{2}-2x-3}{x+1}$的值为0,则x=3或x=-1.其中答案完全正确的题目有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
8.下表是某校九年级(1)班20名学生某次数学测验的成绩统计表:
(1)若这20名学生的平均分是84分,求x和y的值;
(2)这20名学生的本次测验成绩的众数和中位数分别是多少?
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数(人) | 1 | 5 | x | y | 2 |
(2)这20名学生的本次测验成绩的众数和中位数分别是多少?
15.下列说法正确的是( )
| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 相等的角是对顶角 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,垂直于同一直线的两条直线平行 |
10. E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为( )
E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为( )
 E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为( )
E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为( )| A. | 25 | B. | 12 | C. | 13 | D. | 19 |
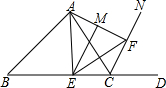 如图,△ABC中,∠ACB=60°,点D在射线BC上,CN平分∠ACD,点F为CN上任意一点,连接AF,M为AF中点,过点M作EM⊥AF交BC于点E,连接AE、FE,探究∠EAC与∠EFC之间的数量关系.
如图,△ABC中,∠ACB=60°,点D在射线BC上,CN平分∠ACD,点F为CN上任意一点,连接AF,M为AF中点,过点M作EM⊥AF交BC于点E,连接AE、FE,探究∠EAC与∠EFC之间的数量关系.