题目内容
5.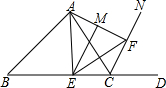 如图,△ABC中,∠ACB=60°,点D在射线BC上,CN平分∠ACD,点F为CN上任意一点,连接AF,M为AF中点,过点M作EM⊥AF交BC于点E,连接AE、FE,探究∠EAC与∠EFC之间的数量关系.
如图,△ABC中,∠ACB=60°,点D在射线BC上,CN平分∠ACD,点F为CN上任意一点,连接AF,M为AF中点,过点M作EM⊥AF交BC于点E,连接AE、FE,探究∠EAC与∠EFC之间的数量关系.
分析 延长AC1至点G,使CG=CF,连接EG;先由SAS证明△ECG≌△ECF,得出∠G=∠EFC,EG=EF,再由线段垂直平分线的性质得出AE=EF,证出AE=EG,由等腰三角形的性质得出∠EAC=∠G,即可得出结论.
解答 解:∠EAC=∠EFC;理由如下:
延长AC1至点G,使CG=CF,连接EG,如图所示: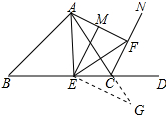
∵∠ACB=60°,
∴∠ECG=∠ACD=120°,
∵CN平分∠ACD,
∴∠FCD=60°,
∴∠ECF=120°,
∴∠ECG=∠ECF,
在△ECG和△ECF中,$\left\{\begin{array}{l}{CG=CF}&{\;}\\{∠ECG=∠ECF}&{\;}\\{EC=EC}&{\;}\end{array}\right.$,
∴△ECG≌△ECF(SAS),∠G=∠EFC,EG=EF,
∵M为AF中点,EM⊥AF,
∴EM垂直平分AF,
∴AE=EF,
∴AE=EG,
∴∠EAC=∠G,
∴∠EAC=∠EFC.
点评 本题考查了全等三角形的判定与性质、线段垂直平分线的性质、等腰三角形的判定与性质;熟练掌握全等三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
16.计算2sin30°-sin245°+tan30°的结果是( )
| A. | $\frac{1}{2}$+3$\sqrt{3}$ | B. | $\frac{1}{2}$+$\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$+$\sqrt{2}$ | D. | 1-$\sqrt{3}$+$\sqrt{2}$ |
17.今年元月份姜老师到银行开户,存入6000元钱,以后的每月根据收入情况存入一笔钱,下表为姜老师从2月份到7月份的存款情况:(超出上月记为正)
根据记录,从2月份至7月份中4月份存入的钱最多.
| 月份 | 2 | 3 | 4 | 5 | 6 | 7 |
| 与上一月比较(元) | -200 | +450 | +400 | -300 | -100 | -600 |
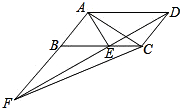 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是①②⑤.
如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是①②⑤.