题目内容
 如图,已知直线y=-x+4与反比例函数y=
如图,已知直线y=-x+4与反比例函数y=| m |
| x |
(1)如果点A的横坐标为1,利用函数图象求关于x的不等式4-x<
| m |
| x |
(2)点P(1,0),设△PAB的面积为S,当S=3时,试求m的值.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据点A在一次函数图象上,可得出点A坐标,再求反比例函数的解析式,从而得出点B坐标,根据图象可得出关于x的不等式4-x<
的解集;
(2)设B(m,n),由y=
(m>0,x>0)关于y=x成轴对称图形,可得出A(n,m),因为S=S△PAC-S△PBC,即可得出m-n=2,又B(m,n)在y=-x+4上,即可得出m的值.
| m |
| x |
(2)设B(m,n),由y=
| m |
| x |
解答:解:(1)点A在y=-x+4上,当x=1时,y=3,
∴A(1,3)
∵点A在y=
上,
∴m=3,
∴y=
(x>0)
由
=-x+4得x1=1,x2=3;
∴点B坐标(3,1),
由图象可得,当x<1或x>3,函数y=-x+4的图象在y=
的下方
∴不等式4-x<
的解集是:0<x<1或x>3;
(2)设B(m,n),由y=
(m>0,x>0)关于y=x成轴对称图形,
∴A(n,m)
∴S=S△PAC-S△PBC=
•m•(4-1)-
•n•(4-1)=
(m-n)=3,
∴m-n=2,
又∵B(m,n)在y=-x+4上,
∴n=-m+4,
∴m=3.
∴A(1,3)
∵点A在y=
| m |
| x |
∴m=3,
∴y=
| 3 |
| x |
由
| 3 |
| x |
∴点B坐标(3,1),
由图象可得,当x<1或x>3,函数y=-x+4的图象在y=
| 3 |
| x |
∴不等式4-x<
| 3 |
| x |
(2)设B(m,n),由y=
| m |
| x |
∴A(n,m)
∴S=S△PAC-S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴m-n=2,
又∵B(m,n)在y=-x+4上,
∴n=-m+4,
∴m=3.
点评:本题考查了反比例函数和一次函数的交点问题,待定系数法求一次函数的解析式和反比例函数的解析式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
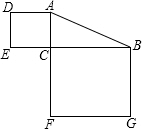 如图,在Rt△ABC中,∠C=90°,若AB=13,则正方形ACED和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=13,则正方形ACED和正方形BCFG的面积和为( )| A、150 | B、169 |
| C、225 | D、无法计算 |
根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量比为2:5,每天生产这种消毒液22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?设应该分装大小瓶两种产品x瓶、y瓶,则可用二元一次方程组表示题中的数量关系为( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|

 已知:如图,反比例函数y=
已知:如图,反比例函数y=