题目内容
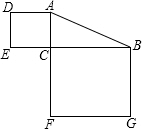如图，在Rt△ABC中，∠C=90°，若AB=13，则正方形ACED和正方形BCFG的面积和为（ ）| A、150 | B、169 |
| C、225 | D、无法计算 |
考点：勾股定理
专题：
分析：小正方形的面积为AC的平方，大正方形的面积为BC的平方．两正方形面积的和为AC2+BC2，对于Rt△ABC，由勾股定理得AB2=AC2+BC2．AB长度已知，故可以求出两正方形面积的和．
解答：解：正方形ACED的面积为：AC2，
正方形BCFG的面积为：BC2；
在Rt△ABC中，AB2=AC2+BC2，AB=13，
则AC2+BC2=169．
故选：B．
正方形BCFG的面积为：BC2；
在Rt△ABC中，AB2=AC2+BC2，AB=13，
则AC2+BC2=169．
故选：B．
点评：本题考查了勾股定理．勾股定理应用的前提条件是在直角三角形中．
练习册系列答案
相关题目
如图，△DEF是由△ABC经过平移得到的，若∠C=80°，∠E=53°，则∠F=
如图，△ABO中，AB⊥OB，OB=下列运算正确的是（ ）
| A、2x+3y=5xy |
| B、（a-b）2=a2-b2 |
| C、5m2•m3=5m5 |
| D、m2•m3=m6 |
如图，已知直线y=-x+4与反比例函数y=
如图，有三条线段AB、BD、DC，AB=6，BD=8，DC=2，且AB∥DC．点E和点F分别为BD上的两个动点，且
如图，在平面直角坐标系中，AB∥CD∥x轴，BC∥DE∥y轴，且AB=CD=4cm，OA=5cm，DE=2cm，动点P从点A出发，沿A→B→C路线运动到点C停止；动点Q从点O出发，沿O→E→D→C路线运动到点C停止；若P、Q两点同时出发，且点P的运动速度为1cm/s，点Q的运动速度为2cm/s．