题目内容
如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后
得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.

(1)求点M、A、B坐标;
(2)连结AB、AM、BM,求∠ABM的正切值;
(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.
见解析
【解析】
试题分析:(1)根据函数平移的规律可得平移后的抛物线解析式是y=(x-1)2-3,所以顶点M的坐标(1,-3),把x=0, x=3分别代入y=(x-1)2-3可求出A点的坐标(0,-2)和点B的坐标(3,1);
(2)过点B作BE⊥AO于E,过点M作MF⊥AO于M,根据EB=EA=3得∠EAB=∠EBA=45°,同理求出∠FAM=∠FMA=45°,然后根据△ABE∽△AMF求出 即可;(3)过点P作PH⊥x轴于H,分两种情况讨论:点P在x轴的上方和下方.
即可;(3)过点P作PH⊥x轴于H,分两种情况讨论:点P在x轴的上方和下方.
试题解析:(1)抛物线y=x2-3向右平移一个单位后得到的函数解析式为y=(x-1)2-3,
顶点M(1,-3),
令x=0,则y=(0-1)2-3=-2,
点A(0,-2),
x=3时,y=(3-1)2-3=4-3=1,
点B(3,1);
(2)过点B作BE⊥AO于E,过点M作MF⊥AO于M,

∵EB=EA=3,
∴∠EAB=∠EBA=45°,
同理可求∠FAM=∠FMA=45°,
∴△ABE∽△AMF,
∴ =
= =
= ,
,
又∵∠BAM=180°-45°×2=90°,
∴tan∠ABM= =
= ;
;
(3)过点P作PH⊥x轴于H,
∵y=(x-1)2-3=x2-2x-2,
∴设点P(x,x2-2x-2),
①点P在x轴的上方时, =
= ,
,
整理得,3x2-7x-6=0,
解得x1=- (舍去),x2=3,
(舍去),x2=3,
∴点P的坐标为(3,1);
②点P在x轴下方时, =
= ,
,
整理得,3x2-5x-6=0,
解得x1= (舍去),x2=
(舍去),x2= ,
,
x= 时,x2-2x-2=-
时,x2-2x-2=- ×
× =-
=- ,
,
∴点P的坐标为( ,-
,- ),
),
综上所述,点P的坐标为(3,1)或( ,-
,- ).
).
考点:1.二次函数图象的平移;2.求抛物线与坐标轴的交点;3.相似三角形的判定与性质;4.锐角三角形函数.

 的方程
的方程 ,下列说法正确的是( )
,下列说法正确的是( )  时,方程无解
时,方程无解  时,方程有一个实数解
时,方程有一个实数解 时,方程有两个相等的实数解
时,方程有两个相等的实数解  时,方程总有两个不相等的实数解
时,方程总有两个不相等的实数解 , ∠ADC=45°,DC=6,求BD的长.
, ∠ADC=45°,DC=6,求BD的长.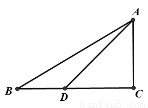
 .
.