题目内容
解方程：
（1）x2-4x-12=0；
（2）（x+3）2=2（x+3）．
（1）x2-4x-12=0；
（2）（x+3）2=2（x+3）．
考点：解一元二次方程-因式分解法
专题：计算题
分析：两方程利用因式分解法求出解即可．
解答：解：（1）方程分解因式得：（x+2）（x-6）=0，
可得x+2=0或x-6=0，
解得：x1=-2，x2=6；
（2）方程变形得：（x+3）2-2（x+3）=0，
分解因式得：（x+3）（x+1）=0，
可得x+3=0或x+1=0，
解得：x1=-3，x2=-1．
可得x+2=0或x-6=0，
解得：x1=-2，x2=6；
（2）方程变形得：（x+3）2-2（x+3）=0，
分解因式得：（x+3）（x+1）=0，
可得x+3=0或x+1=0，
解得：x1=-3，x2=-1．
点评：此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
快捷英语周周练系列答案
相关题目
已知a=x+3，b=x+1，c=x+2，则代数式a2+b2+c2-ab-bc-ac的值是（ ）
| A、4 | B、3 | C、2 | D、1 |
已知：如图，已知直线AB，CD被直线GH所截，直线PQ、MN分别过点E、F，如果AB∥CD，那么由下列条件不能推出MN∥PQ的是（ ）| A、∠1=∠2 |
| B、∠3=∠4 |
| C、∠2=∠3 |
| D、∠PEG=∠MFG |
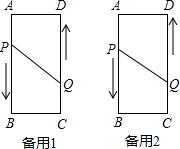如图，长方形ABCD（长方形的对边相等，每个角都是90°），AB=6cm，AD=2cm，动点P、Q分别从点A、C同时出发，点P以2厘米/秒的速度向终点B移动，点Q以1厘米/秒的速度向D移动，当有一点到达终点时，另一点也停止运动．设运动的时间为t，问：
如图，?ABCD中，∠ABC=60°，E、F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，AB=2，求CF的长．
如图，Rt△ABC中，∠B=30°，BC=12cm，求AC的长．