Question

12．如图，直线AB、CD相交于点O，OE平分∠BOD．
（1）若∠AOC=70°，∠DOF=90°，求∠EOF的度数；
（2）若OF平分∠COE，∠BOF=15°，若设∠AOE=x°．
①则∠EOF=$\frac{1}{2}x$．（用含x的代数式表示）
②求∠AOC的度数．

Answer 1

分析 （1）由对顶角的性质可知∠BOD=70°，从而可求得∠FOB=20°，由角平分线的定义可知∠BOE=$\frac{1}{2}$∠BOD，最后根据∠EOF=∠BOE+∠FOB求解即可；
（2）①先证明∠AOE=∠COE=x，然后由角平分线的定义可知∠FOE=$\frac{1}{2}x$；
②∠BOE=∠FOE-∠FOB可知∠BOE=$\frac{1}{2}$x-15°，最后根据∠BOE+∠AOE=180°列出方程可求得x的值，从而可求得∠AOC的度数．

解答 解：（1）由对顶角相等可知：∠BOD=∠AOC=70°，
∵∠FOB=∠DOF-∠BOD，
∴∠FOB=90°-70°=20°，
∵OE平分∠BOD，
∴∠BOE=$\frac{1}{2}$∠BOD=$\frac{1}{2}$×70°=35°，
∴∠EOF=∠FOB+∠BOE=35°+20°=55°，
（2）①∵OE平分∠BOD，
∴∠BOE=∠DOE，
∵∠BOE+∠AOE=180°，∠COE+∠DOE=180°，
∴∠COE=∠AOE=x，
∵OF平分∠COE，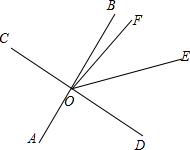
∴∠FOE=$\frac{1}{2}$x，
故答案为：$\frac{1}{2}x$；
②∵∠BOE=∠FOE-∠FOB，
∴∠BOE=$\frac{1}{2}$x-15°，
∵∠BOE+∠AOE=180°，
∴$\frac{1}{2}$x-15°+x=180°，
解得：x=130°，
∴∠AOC=2∠BOE=2×（180°-130°）=100°．

点评 本题考查了对顶角，角平分线定义，角的有关定义的应用，主要考查学生的计算能力．