Question

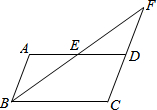如图，在?ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F．
（1）证明：FD=AB；
（2）当?ABCD的面积为8时，求△FED的面积．

Answer 1

考点：平行四边形的性质,全等三角形的判定与性质

专题：

分析：（1）利用已知得出△ABE≌△DFE（AAS），进而求出即可；
（2）首先得出△FED∽△FBC，进而得出

S△FED

S△FBC

=

1

4

，进而求出即可．

解答：（1）证明：∵在平行四边形ABCD中，E是AD边上的中点，
∴AE=ED，∠ABE=∠F，
在△ABE和△DFE中

∠ABE=∠F ∠BEA=∠FED AE=DE

，
∴△ABE≌△DFE（AAS），
∴FD=AB；

（2）解：∵DE∥BC，
∴△FED∽△FBC，
∵△ABE≌△DFE，
∴BE=EF，S_△FBC=S_?ABCD，
∴

EF

BF

=

1

2

，
∴

S△FED

S△FBC

=

1

4

，
∴

S△FED

8

=

1

4

，
∴△FED的面积为：2．

点评：此题主要考查了全等三角形的判定与性质以及平行四边形的性质以及相似三角形的判定与性质等知识，得出S_△FBC=S_{平行四边形ABCD}是解题关键．