题目内容
在△ABC中,∠ACB=90°,AC=BC,点P为△ABC外一点(P与C在直线AB异侧),且∠APB=45°,过点C作CD⊥PA,垂足为D.

(1)求证:PA=2CD;
(2)设点P关于AB的对称点为E,连接PE、CE,试判定线段AB与CE的数量关系,并给予证明.

(1)求证:PA=2CD;
(2)设点P关于AB的对称点为E,连接PE、CE,试判定线段AB与CE的数量关系,并给予证明.
考点:相似形综合题
专题:
分析:(1)根据等腰直角三角形的性质,可得AP与AF的关系,根据相似三角形的判定与性质,可得AF与CD的关系,根据等量代换,可得答案;
(2)根据等腰直角三角形的性质,可得∠ACM=∠BCM=45°,根据两个角对应相等的两个三角形相似,可得△CIN∽△EIB,根据相似三角形的性质,可得对应边的比相等,根据线段垂直平分线的性质,可得NA=NB,根据等腰三角形的判定,可得AC=CE,
(2)根据等腰直角三角形的性质,可得∠ACM=∠BCM=45°,根据两个角对应相等的两个三角形相似,可得△CIN∽△EIB,根据相似三角形的性质,可得对应边的比相等,根据线段垂直平分线的性质,可得NA=NB,根据等腰三角形的判定,可得AC=CE,
解答:证明:(1)过点A作AF⊥BP于点F ,
,
∵∠BPA=45°,
∴∠FAP=∠FPA=45°,
∴
=
,
∴AP=
AF.
∵∠ABF=∠BAP+∠P=∠BAP+45°,
又∵∠CAD=∠BAP+∠CAB=∠BAP+45°
∴∠CAD=∠FBA.
又∵∠ADC=∠AFB=90°
∴△CAD∽△ABF
∴
=
=
∴AF=
CD
∴AP=
AF=2CD;
(2)作CM⊥AB于点M,交AE于点N,连接BN ,
,
∵∠ACB=90°,AC=BC,
∴∠ACM=∠BCM=45°,AB=
AC,
∵∠BAP=45°
又∵点P、点E关于AB对称
∴∠APB=∠AEB=45°,
∴∠BCM=∠AEB=45°.
又∵∠CIN=∠EIB
∴△CIN∽△EIB
∴
=
,
∴
=
,
又∵∠CIE=∠NIB
∴△NIB∽△CIE
∴∠CEI=∠IBN
∵CM⊥AB,AM=MB,相似三角形的判定与性质,
∴NA=NB,
∴∠NAB=∠NBA,
∴∠CAN=∠CBN,
∴∠CAE=∠CEA,
∴CA=CE.
又∵AB=
AC,
∴AB=
CE.
 ,
,∵∠BPA=45°,
∴∠FAP=∠FPA=45°,
∴
| AP |
| AF |
| 2 |
∴AP=
| 2 |
∵∠ABF=∠BAP+∠P=∠BAP+45°,
又∵∠CAD=∠BAP+∠CAB=∠BAP+45°
∴∠CAD=∠FBA.
又∵∠ADC=∠AFB=90°
∴△CAD∽△ABF
∴
| AF |
| CD |
| AB |
| AC |
| 2 |
∴AF=
| 2 |
∴AP=
| 2 |
(2)作CM⊥AB于点M,交AE于点N,连接BN
 ,
,∵∠ACB=90°,AC=BC,
∴∠ACM=∠BCM=45°,AB=
| 2 |
∵∠BAP=45°
又∵点P、点E关于AB对称
∴∠APB=∠AEB=45°,
∴∠BCM=∠AEB=45°.
又∵∠CIN=∠EIB
∴△CIN∽△EIB
∴
| CI |
| EI |
| NI |
| BI |
∴
| CI |
| NI |
| EI |
| BI |
又∵∠CIE=∠NIB
∴△NIB∽△CIE
∴∠CEI=∠IBN
∵CM⊥AB,AM=MB,相似三角形的判定与性质,
∴NA=NB,
∴∠NAB=∠NBA,
∴∠CAN=∠CBN,
∴∠CAE=∠CEA,
∴CA=CE.
又∵AB=
| 2 |
∴AB=
| 2 |
点评:本题考查了相似形综合题,利用了等腰直角三角形的性质,相似三角形的判定与性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实数a、b满足
(
+2b)=2
+3b,则
的值为( )
|
| ab |
| ab |
| a |
| b |
| A、1或9 | B、1或3 |
| C、1或3或9 | D、不存在 |

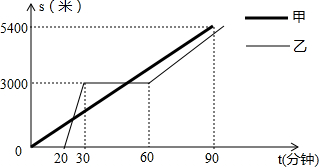 某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据以上信息回答下列问题:
某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据以上信息回答下列问题: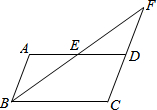 如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.