题目内容
13.计算:(1)$\frac{2{x}^{2}}{3{y}^{2}}$•$\frac{5y}{6x}$÷$\frac{10y}{21{x}^{2}}$
(2)$\frac{3}{{x}^{2}-9}$-$\frac{1}{2x-6}$
(3)$\frac{{a}^{2}}{a-1}$-a-1
(4)$\frac{1}{x+1}$-$\frac{1}{{x}^{2}-1}$÷$\frac{x+1}{{x}^{2}-2x+1}$.
分析 (1)原式利用除法法则变形,约分即可得到结果;
(2)原式两项通分并利用同分母分式的减法法则计算即可得到结果;
(3)原式通分并利用同分母分式的减法法则计算即可得到结果;
(4)原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=$\frac{2{x}^{2}}{3{y}^{2}}$•$\frac{5y}{6x}$•$\frac{21{x}^{2}}{10y}$=$\frac{7{x}^{3}}{6{y}^{2}}$;
(2)原式=$\frac{6}{2(x+3)(x-3)}$-$\frac{x+3}{2(x+3)(x-3)}$=$\frac{-(x-3)}{2(x+3)(x-3)}$=-$\frac{1}{2(x+3)}$;
(3)原式=$\frac{{a}^{2}-(a+1)(a-1)}{a-1}$=$\frac{1}{a-1}$;
(4)原式=$\frac{1}{x+1}$-$\frac{1}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+1}$=$\frac{1}{x+1}$-$\frac{x-1}{(x+1)^{2}}$=$\frac{x+1-x+1}{(x+1)^{2}}$=$\frac{2}{(x+1)^{2}}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
4.若函数$y=(m-1){x^{{m^2}-2}}$为反比例函数,则m的值为( )
| A. | ±1 | B. | 1 | C. | $\sqrt{3}$ | D. | -1 |
8.甲队在m天内挖水渠a米,乙队在n天内挖水渠b米,两队合挖s米水渠,需要的天数为( )
| A. | $\frac{smn}{an+bm}$ | B. | $\frac{sm}{a}$+$\frac{sn}{b}$ | C. | $\frac{sab}{an+bm}$ | D. | $\frac{am}{a+b}$ |
18.x7等于( )
| A. | (-x2)•x5 | B. | (-x)3x4 | C. | (-x2)•(-x5) | D. | (-x)(-x)6 |
5.下列运算正确的是( )
| A. | x3•x2=x6 | B. | (ab)2=ab2 | C. | (-m2)3=-m6 | D. | p6÷p3=2 |
2.以下两条直线互相垂直的是( )
①两条直线相交所成的四个角中有一个是直角;
②两条直线相交所成的四个角相等;
③两条直线相交,有一组邻补角相等;
④两条直线相交,对顶角互补.
①两条直线相交所成的四个角中有一个是直角;
②两条直线相交所成的四个角相等;
③两条直线相交,有一组邻补角相等;
④两条直线相交,对顶角互补.
| A. | ①③ | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
3.下列说法正确的是( )
| A. | 81的算术平方根是9 | B. | 81的平方根是-9 | ||
| C. | -81的平方根是9 | D. | 49的算术平方根是±7 |
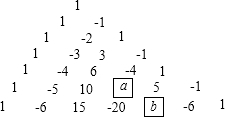
 如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为( )
如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为( )