题目内容
18.x7等于( )| A. | (-x2)•x5 | B. | (-x)3x4 | C. | (-x2)•(-x5) | D. | (-x)(-x)6 |
分析 A:根据同底数幂的乘法法则判断即可.
B:首先根据积的乘方的运算方法,求出(-x)3的值是多少,然后把求出的结果乘以x4即可.
C:根据同底数幂的乘法法则判断即可.
D:首先根据积的乘方的运算方法,求出(-x)6的值是多少,然后把求出的结果和-x相乘即可.
解答 解:∵(-x2)•x5=-x7,
∴选项A不正确;
∵(-x)3x4=(-x3)•x4=-x7,
∴选项B不正确;
∵(-x2)•(-x5)=x7,
∴选项C正确;
∵(-x)(-x)6=(-x)•x6=-x7,
∴选项D不正确.
故选:C.
点评 (1)此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数),解答此题的关键是判断出26=82.
(2)此题还考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.

练习册系列答案
相关题目
9.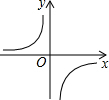 已知函数$y=\frac{m}{x}$图象如图,以下结论,其中正确有( )个:
已知函数$y=\frac{m}{x}$图象如图,以下结论,其中正确有( )个:
①m<0;
②在每个分支上y随x的增大而增大;
③若A(-1,a),点B(2,b)在图象上,则a<b
④若P(x,y)在图象上,则点P1(-x,-y)也在图象上.
 已知函数$y=\frac{m}{x}$图象如图,以下结论,其中正确有( )个:
已知函数$y=\frac{m}{x}$图象如图,以下结论,其中正确有( )个:①m<0;
②在每个分支上y随x的增大而增大;
③若A(-1,a),点B(2,b)在图象上,则a<b
④若P(x,y)在图象上,则点P1(-x,-y)也在图象上.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
10.已知a=-(0.2)2,b=-22,c=(-$\frac{1}{2}$)-2,d=(-$\frac{1}{2}$)0,则比较a、b、c、d的大小结果是( )
| A. | a<b<c<d | B. | a<b<d<c | C. | b<a<d<c | D. | b<a<c<d |
 如图所示,已知a∥b,BC⊥CD,点C在直线b上.若∠α=20°,则∠β=70°.
如图所示,已知a∥b,BC⊥CD,点C在直线b上.若∠α=20°,则∠β=70°. 如图:BC⊥AC,BC=8cm,AB=10cm,AC=6cm,那么点B到AC的距离为8cm.
如图:BC⊥AC,BC=8cm,AB=10cm,AC=6cm,那么点B到AC的距离为8cm.