题目内容
1．
如图，在等边三角形ABC中，AB=6，D是BC上一点，且BC=3BD，△ABD绕点A旋转后得到△ACE，则CE的长度为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 6 |
分析 由等边三角形的性质得出BC=AB=6，求出BD，由旋转的性质得出△ACE≌△ABD，得出CE=BD，即可得出结果．
解答 解：∵△ABC是等边三角形，
∴BC=AB=6，
∵BC=3BD，
∴BD=$\frac{1}{3}$BC=2，
由旋转的性质得：△ACE≌△ABD，
∴CE=BD=2．
故选：A．
点评 本题考查了旋转的性质、等边三角形的性质、全等三角形的性质；熟练掌握旋转的性质和等边三角形的性质是解决问题的关键．
练习册系列答案
相关题目
9．
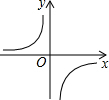已知函数$y=\frac{m}{x}$图象如图，以下结论，其中正确有（ ）个：
①m＜0；
②在每个分支上y随x的增大而增大；
③若A（-1，a），点B（2，b）在图象上，则a＜b
④若P（x，y）在图象上，则点P1（-x，-y）也在图象上．
已知函数$y=\frac{m}{x}$图象如图，以下结论，其中正确有（ ）个：①m＜0；
②在每个分支上y随x的增大而增大；
③若A（-1，a），点B（2，b）在图象上，则a＜b
④若P（x，y）在图象上，则点P1（-x，-y）也在图象上．
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
如图所示，已知a∥b，BC⊥CD，点C在直线b上．若∠α=20°，则∠β=70°．
10．已知a=-（0.2）2，b=-22，c=（-$\frac{1}{2}$）-2，d=（-$\frac{1}{2}$）0，则比较a、b、c、d的大小结果是（ ）
| A． | a＜b＜c＜d | B． | a＜b＜d＜c | C． | b＜a＜d＜c | D． | b＜a＜c＜d |