题目内容
1.按要求完成下列各小题.(1)当a=41,b=40时,求a2-b2的平方根;
(2)当a=$\sqrt{9}$,b=$\root{3}{-27}$时,求a+b的立方根.
分析 (1)把a与b的值代入原式计算即可得到结果;
(2)利用算术平方根及立方根定义计算求出a与b的值,即可求出a+b的立方根.
解答 解:(1)原式=(a+b)(a-b)=81,
则81的平方根为9或-9;
(2)∵a=$\sqrt{9}$=3,b=$\root{3}{-27}$=-3,
∴a+b=0,
则a+b的平方根为0.
点评 此题考查了立方根,算术平方根,以及平方根,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
16. 如图,在平面直角坐标系中有P,Q两点,其坐标分别为(5,a),(b,7),根据图中P,Q两点的位置可判断,点(6-b,a-10)落在( )
如图,在平面直角坐标系中有P,Q两点,其坐标分别为(5,a),(b,7),根据图中P,Q两点的位置可判断,点(6-b,a-10)落在( )
 如图,在平面直角坐标系中有P,Q两点,其坐标分别为(5,a),(b,7),根据图中P,Q两点的位置可判断,点(6-b,a-10)落在( )
如图,在平面直角坐标系中有P,Q两点,其坐标分别为(5,a),(b,7),根据图中P,Q两点的位置可判断,点(6-b,a-10)落在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.计算1+2+22+23+…+22014的值为( )
| A. | 22015-1 | B. | 22015+1 | C. | $\frac{1}{2}$(22015-1) | D. | $\frac{1}{2}$(22015+1) |
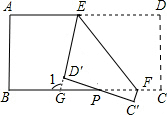 如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠BFC′=70°,则∠1=110°.
如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠BFC′=70°,则∠1=110°. 如图,四边形ABCD中,AD∥BC,∠A=90°,点F为AB上一点,DF⊥CD,BE⊥CD于E,DF=BF,求证:
如图,四边形ABCD中,AD∥BC,∠A=90°,点F为AB上一点,DF⊥CD,BE⊥CD于E,DF=BF,求证: