题目内容
1.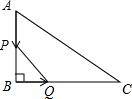 如图,在△ABC中,∠B=90°,BC=8cm,AC=10cm,动点A从点A出发以1cm/s的速度沿AB边运动,同时动点Q从点B出发以2cm/s的速度沿BC边运动.设运动时间为t秒.
如图,在△ABC中,∠B=90°,BC=8cm,AC=10cm,动点A从点A出发以1cm/s的速度沿AB边运动,同时动点Q从点B出发以2cm/s的速度沿BC边运动.设运动时间为t秒.(1)若△PBQ的面积等于8cm2,求t的值;
(2)若PQ的长等于$\sqrt{29}$cm,求t的值.
分析 (1)由题意,利用勾股定理求得AB=6,可设P、Q经过t秒,使△PBQ的面积为8cm2,则PB=6-t,BQ=2t,根据三角形面积的计算公式,S△PBQ=$\frac{1}{2}$BQ•PB,列出方程,解答出即可;
(2)可设P、Q两点运动t秒时,则PB=6-t,BQ=2t,根据勾股定理,可得PQ2=BP2+BQ2,代入整理即可求出.
解答 解:(1)AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=6,
设P、Q经过t秒时,△PBQ的面积为8cm2,
则PB=6-t,BQ=2t,
∵∠B=90°,AB=6cm,BC=8cm,
∴,$\frac{1}{2}$(6-t)2t=8,
解得,t1=2,t2=4,
∴当P、Q经过2或4秒时,△PBQ的面积为8cm2;
(2)设P、Q两点运动t秒时,PQ的长等于$\sqrt{29}$cm,
则29=(6-t)2+(2t)2,
解得:t1=1,t2=$\frac{7}{5}$,
答:当t为1或$\frac{7}{5}$时,PQ的长等于$\sqrt{29}$cm.
点评 此题考查一元二次方程的实际运用,勾股定理的实际运用,利用三角形的面积和勾股定理建立方程是解决问题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,在平面直角坐标系中,直线y=2x+m与y轴交于点A,与直线y=-x+4交于点B(3,n),P为直线y=-x+4与y轴的交点.
如图,在平面直角坐标系中,直线y=2x+m与y轴交于点A,与直线y=-x+4交于点B(3,n),P为直线y=-x+4与y轴的交点. 如图所示,四边形ABCD和四边形CEFG均为正方形.
如图所示,四边形ABCD和四边形CEFG均为正方形.