题目内容
16．
如图，在平面直角坐标系中，直线y=2x+m与y轴交于点A，与直线y=-x+4交于点B（3，n），P为直线y=-x+4与y轴的交点．（1）求m，n的值；
（2）求三角形APB的面积．
分析 （1）首先把点B（3，n）代入直线y=-x+4得出n的值，再进一步代入直线y=2x+m求得m的值即可；
（2）求得A、P点坐标，进一步利用三角形的面积求得答案即可．
解答 解：（1）∵点B（3，n）在直线上y=-x+4，
∴n=1，B（3，1）
∵点B（3，1）在直线上y=2x+m上，
∴m=-5．
（2）直线y=2x-5与y轴交于点A，
A点坐标为（0，-5），
P为直线y=-x+4与y轴的交点，
P点坐标为（0，4）
三角形APB的面积=$\frac{1}{2}$×（4+5）×3=$\frac{27}{2}$．
点评 本题考查了两条直线相交问题，掌握一次函数与y轴的交点坐标的求法是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．若$\frac{a}{b}$=$\frac{c}{d}$=$\frac{m}{n}$=$\frac{1}{2}$，则$\frac{a-2c+3m}{b-2d+3n}$=$\frac{1}{2}$．
11．某中学七年级（1）班学生期末数学平均成绩90分．
（1）下表给出了该班6名同学的成绩情况，试完成下表．
（2）谁的成绩最好？谁的成绩最差？
（3）成绩最好的比成绩最差的高多少分？
（1）下表给出了该班6名同学的成绩情况，试完成下表．
| 姓名 | 小新 | 小雪 | 小丽 | 丁丁 | 小天 | 小亮 |
| 成绩 | 88 | 90 | 86 | 100 | 85 | |
| 成绩与平均成绩的差值 | +1 | -2 | 0 | -4 | +10 | -5 |
（3）成绩最好的比成绩最差的高多少分？
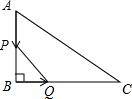如图，在△ABC中，∠B=90°，BC=8cm，AC=10cm，动点A从点A出发以1cm/s的速度沿AB边运动，同时动点Q从点B出发以2cm/s的速度沿BC边运动．设运动时间为t秒．