题目内容
12．下列方程：①$\frac{x}{5}=2$；②$\frac{5}{x}$=2；③y=$\frac{2}{3}$x；④$\frac{1+x}{5+x}$=$\frac{1}{2}$；⑤y+1=$\frac{2}{y}$；⑥1+3（x-2）=7-x；⑦y2-3=$\frac{y}{3}$．其中，分式方程有（ ）个．| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据分式方程的定义：分母里含有字母的方程叫做分式方程进行判断即可．
解答 解：下列方程：①$\frac{x}{5}=2$；②$\frac{5}{x}$=2；③y=$\frac{2}{3}$x；④$\frac{1+x}{5+x}$=$\frac{1}{2}$；⑤y+1=$\frac{2}{y}$；⑥1+3（x-2）=7-x；⑦y2-3=$\frac{y}{3}$是分式方程的是：②④⑤，共3个；
故选C．
点评 此题考查了分式方程的定义，判断一个方程是否为分式方程，主要是依据分式方程的定义，也就是看分母中是否含有未知数（注意：仅仅是字母不行，必须是表示未知数的字母）．
练习册系列答案
相关题目
3．在2015，6，$2\frac{1}{2}$，0，-3，+1，$-\frac{1}{4}$中，负数共有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 6个 |
如图所示，一根长2a的木棍（AB），斜靠在与地面（OM）垂直的墙（ON）上，设木棍的中点为P，若木棍A端沿墙下滑，且B端沿地面向右滑行．请判断木棍滑动的过程中，点P到点O的距离不发生变化（用“发生”或“不发生”填空）．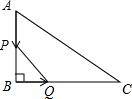
如图，在△ABC中，∠B=90°，BC=8cm，AC=10cm，动点A从点A出发以1cm/s的速度沿AB边运动，同时动点Q从点B出发以2cm/s的速度沿BC边运动．设运动时间为t秒．