题目内容
为增强居民节约用电意识,某市对居民用电实行“阶梯收费”,具体收费标准见表:
某居民五月份用电190千瓦时,缴纳电费90元.
(1)求x和超出部分电费单价;
(2)若该户居民六月份所缴电费不低于75元且不超过84元,求该户居民六月份的用电量范围.
| 一户居民一个月用电量的范围 | 电费价格(单位:元/千瓦时) |
| 不超过160千瓦时的部分 | x |
| 超过160千瓦时的部分 | x+0.15 |
(1)求x和超出部分电费单价;
(2)若该户居民六月份所缴电费不低于75元且不超过84元,求该户居民六月份的用电量范围.
考点:一元一次不等式的应用,一元一次方程的应用
专题:应用题
分析:(1)等量关系为:不超过160千瓦时电费+超过160千瓦时电费=90;
(2)设该户居民六月份的用电量是a千瓦时.则依据收费标准列出不等式75≤160×0.45+0.6(a-160)≤84.
(2)设该户居民六月份的用电量是a千瓦时.则依据收费标准列出不等式75≤160×0.45+0.6(a-160)≤84.
解答:解:(1)根据题意,得
160x+(190-160)(x+0.15)=90,
解得 x=0.45;
则超出部分的电费单价是x+0.15=0.6(元/千瓦时).
答:x和超出部分电费单价分别是0.45和0.6元/千瓦时;
(2)设该户居民六月份的用电量是a千瓦时.则
75≤160×0.45+0.6(a-160)≤84,
解得 165≤a≤180.
答:该户居民六月份的用电量范围是165度到180度.
160x+(190-160)(x+0.15)=90,
解得 x=0.45;
则超出部分的电费单价是x+0.15=0.6(元/千瓦时).
答:x和超出部分电费单价分别是0.45和0.6元/千瓦时;
(2)设该户居民六月份的用电量是a千瓦时.则
75≤160×0.45+0.6(a-160)≤84,
解得 165≤a≤180.
答:该户居民六月份的用电量范围是165度到180度.
点评:本题考查了一元一次不等式的应用,一元一次方程的应用.解答本题的关键是读懂题意,设出未知数,找出等量(不等量)关系,列方程(不等式)求解.

练习册系列答案
相关题目
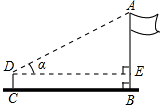 某校九年级四个数学活动小组参加测量操场旗杆高度的综合实践活动,如图是四个小组在不同位置测量后绘制的示意图,用测角仪测得旗杆顶端A的仰角记为α,CD为测角仪的高,测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB,四个小组测量和计算数据如下表所示:
某校九年级四个数学活动小组参加测量操场旗杆高度的综合实践活动,如图是四个小组在不同位置测量后绘制的示意图,用测角仪测得旗杆顶端A的仰角记为α,CD为测角仪的高,测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB,四个小组测量和计算数据如下表所示: 如图,面积为70cm2的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的周长为
如图,面积为70cm2的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的周长为 根据如图所示程序计算函数值,若输入的x的值为
根据如图所示程序计算函数值,若输入的x的值为