题目内容
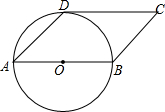 如图,四边形ABCD是平行四边形,AB=2,以边AB为直径的⊙O经过点D,且∠DAB=45°.
如图,四边形ABCD是平行四边形,AB=2,以边AB为直径的⊙O经过点D,且∠DAB=45°.(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若以C为圆心的⊙C与⊙O相切,求⊙C的半径.
考点:切线的判定与性质,勾股定理,平行四边形的性质
专题:
分析:(1)连接OD,即可得∠BOD=90°,又由四边形ABCD是平行四边形,可得AB∥DC,即可求得OD⊥CD,则可得CD与⊙O的位置关系是相切;
(2)作CE⊥OB,交OB的延长线于点E,连接OC,由四边形ABCD是平行四边形,可得AD∥BC,可得∠CBE=∠DAB=45°,然后在Rt△OCE中,由勾股定理即可求得OC的值,从而求得⊙C的半径.
(2)作CE⊥OB,交OB的延长线于点E,连接OC,由四边形ABCD是平行四边形,可得AD∥BC,可得∠CBE=∠DAB=45°,然后在Rt△OCE中,由勾股定理即可求得OC的值,从而求得⊙C的半径.
解答: 解:(1)直线CD与⊙O相切.
解:(1)直线CD与⊙O相切.
连接OD.
∵∠DAB=45°,OA=OD,
∴∠ADO=∠DAO=45°,
∴∠DOB=90°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴OD⊥CD,
∵OD为⊙O半径,
∴直线CD与⊙O相切.
(2)作CE⊥OB,交OB的延长线于点E,连接OC.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CBE=∠DAB=45°,四边形DOEC是矩形,
∵AB=2,
∴BE=CE=OD=1.
在Rt△OCE中,OC=
=
,
∵⊙C与⊙O 相切,
∴⊙C的半径为
-1或
+1.
 解:(1)直线CD与⊙O相切.
解:(1)直线CD与⊙O相切. 连接OD.
∵∠DAB=45°,OA=OD,
∴∠ADO=∠DAO=45°,
∴∠DOB=90°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴OD⊥CD,
∵OD为⊙O半径,
∴直线CD与⊙O相切.
(2)作CE⊥OB,交OB的延长线于点E,连接OC.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CBE=∠DAB=45°,四边形DOEC是矩形,
∵AB=2,
∴BE=CE=OD=1.
在Rt△OCE中,OC=
| CE2+OE2 |
| 5 |
∵⊙C与⊙O 相切,
∴⊙C的半径为
| 5 |
| 5 |
点评:此题考查了切线的判定与性质、平行四边形的性质以及勾股定理等知识.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
某市某种出租车收费标准为:起步价6元(3千米以内),3千米后每千米加收1.5元,某人乘坐x(x>3)千米,应付费( )元.
| A、6+1.5x |
| B、6+1.5(x-3) |
| C、6+3x |
| D、1.5x+3 |
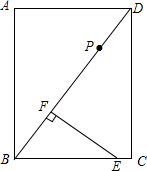 如图,在矩形ABCD中,BC=6cm,AB=8cm,E是BC上的一点,且BE=5cm,过点E作EF⊥BD,垂足为F,点P从D出发沿DB方向向点B运动,速度为1cm/秒,运动时间为t秒.在矩形边上找一点Q,使得以E,F,P,Q为顶点的四边形为平行四边形,则t值为
如图,在矩形ABCD中,BC=6cm,AB=8cm,E是BC上的一点,且BE=5cm,过点E作EF⊥BD,垂足为F,点P从D出发沿DB方向向点B运动,速度为1cm/秒,运动时间为t秒.在矩形边上找一点Q,使得以E,F,P,Q为顶点的四边形为平行四边形,则t值为 如图,在正方形ABCD内作等边△AED,连接BE,求∠EBC的度数.
如图,在正方形ABCD内作等边△AED,连接BE,求∠EBC的度数. 如图是一个8×7的正方形网格图,且每个小正方形的边长为1.
如图是一个8×7的正方形网格图,且每个小正方形的边长为1.