题目内容
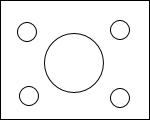 如图,学校有一块长方形空地,它的长与宽的比为5:4,面积为2600平方米.
如图,学校有一块长方形空地,它的长与宽的比为5:4,面积为2600平方米.(1)求该长方形的长与宽(结果保留一位小数)
(2)现要在空地中规划出5个圆形区域进行绿化,圆形区域的总面积为600平方米,其中四周的四个小圆的半径相等,中间大圆的半径为小圆半径的3倍,你能估计出小圆的半径吗(结果保留1位小数).
考点:一元二次方程的应用
专题:几何图形问题
分析:(1)设出边长,运用面积公式列出方程,即可解决问题.
(2)设出小圆的半径,表示出大圆的半径,运用圆形区域的总面积为600平方米列出方程,求解方程,即可解决问题.
(2)设出小圆的半径,表示出大圆的半径,运用圆形区域的总面积为600平方米列出方程,求解方程,即可解决问题.
解答: 解:(1)设长方形的长为5λ,则宽为4λ;
解:(1)设长方形的长为5λ,则宽为4λ;
由题意得:5λ•4λ=2600,
解得:λ≈11.4(米),
∴该长方形的长与宽分别为57米、45.6米.
(2)设小圆的半径为μ,则大圆的半径为3μ,
由题意得:4πμ2+9πμ2=600,
解得:μ≈3.8(米).
 解:(1)设长方形的长为5λ,则宽为4λ;
解:(1)设长方形的长为5λ,则宽为4λ;由题意得:5λ•4λ=2600,
解得:λ≈11.4(米),
∴该长方形的长与宽分别为57米、45.6米.
(2)设小圆的半径为μ,则大圆的半径为3μ,
由题意得:4πμ2+9πμ2=600,
解得:μ≈3.8(米).
点评:该题主要考查了一元二次方程及其在现实生活中的应用问题;解题的关键是深刻把握题意,准确找出命题中隐含的等量关系.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
 如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=3,CD=2.求AB的长.
如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=3,CD=2.求AB的长. 如图所示,若AB∥CD,直线EF与AB、CD分别相交于点E,F,∠FEB与∠EFD的平分线相交于点P,且∠EFD=60°,求∠BEP的度数.
如图所示,若AB∥CD,直线EF与AB、CD分别相交于点E,F,∠FEB与∠EFD的平分线相交于点P,且∠EFD=60°,求∠BEP的度数. 某县“贡江新区”位于贡江南岸(如图),由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局,为建设河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务,由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天.
某县“贡江新区”位于贡江南岸(如图),由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局,为建设河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务,由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天. 已知直线l上有一点O,点A,B同时从O出发,在直线l上分别向左,向右作匀速运动,且A,B的速度之比是1:2,设运动时间为ts,
已知直线l上有一点O,点A,B同时从O出发,在直线l上分别向左,向右作匀速运动,且A,B的速度之比是1:2,设运动时间为ts, 如图,用一根长为22cm的铁丝分段围成一个面积为10cm2的“田”字形的长方形铁丝框.设宽为x,请列出关于x的方程并化成一般形式.
如图,用一根长为22cm的铁丝分段围成一个面积为10cm2的“田”字形的长方形铁丝框.设宽为x,请列出关于x的方程并化成一般形式.