题目内容
10.先阅读,再解题解不等式:$\frac{2x+5}{x-3}>0$
解:根据两数相除,同号得正,异号得负,得
①$\left\{{\begin{array}{l}{2x+5>0}\\{x-3>0}\end{array}}\right.$或 ②$\left\{{\begin{array}{l}{2x+5<0}\\{x-3<0}\end{array}}\right.$
解不等式组①,得x>3
解不等式组②,得x<-$\frac{5}{2}$
根据上述解题过程反映的解题思想方法,解不等式(2x-3)(1+3x)<0.
分析 根据题意列出关于x的不等式组,求出x的取值范围即可.
解答 解:根据两数相除,同号得正,异号得负,得
①$\left\{\begin{array}{l}2x-3>0\\ 1+3x<0\end{array}\right.$,②$\left\{\begin{array}{l}2x-3<0\\ 1+3x>0\end{array}\right.$,
解不等式组①得,不等式组无解;
解不等式组②得,-$\frac{1}{3}$<x<$\frac{3}{2}$.
点评 本题考查的是解一元一次不等式组,根据题意列出关于x的不等式组是解答此题的关键.

练习册系列答案
相关题目
19.下列方程的变形正确的是( )
| A. | 由3+x=5,得x=5+3 | B. | 由7x=-3,得x=-$\frac{7}{3}$ | C. | 由2y=0,得y=$\frac{1}{2}$ | D. | 由-2x-6=0得x=-3 |
20.若不等式ax+x>1+a的解集是x<1,则a必须满足的条件是( )
| A. | a<-1 | B. | a<1 | C. | a>-1 | D. | a>1 |
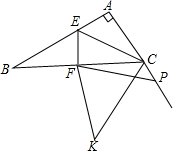 在△ABC中,∠BAC=90°,BC的垂直平分线EF交BC于点F,交AB于点E,P是AC延长线上一点,连接FP,将FP绕点F逆时针旋转2α,得到FK,连接CK,如果∠B=α(0°<α<90°),则$\frac{CK-CP}{cosα•EF}$=2.
在△ABC中,∠BAC=90°,BC的垂直平分线EF交BC于点F,交AB于点E,P是AC延长线上一点,连接FP,将FP绕点F逆时针旋转2α,得到FK,连接CK,如果∠B=α(0°<α<90°),则$\frac{CK-CP}{cosα•EF}$=2.