题目内容
2.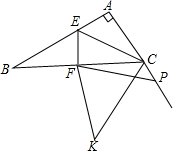 在△ABC中,∠BAC=90°,BC的垂直平分线EF交BC于点F,交AB于点E,P是AC延长线上一点,连接FP,将FP绕点F逆时针旋转2α,得到FK,连接CK,如果∠B=α(0°<α<90°),则$\frac{CK-CP}{cosα•EF}$=2.
在△ABC中,∠BAC=90°,BC的垂直平分线EF交BC于点F,交AB于点E,P是AC延长线上一点,连接FP,将FP绕点F逆时针旋转2α,得到FK,连接CK,如果∠B=α(0°<α<90°),则$\frac{CK-CP}{cosα•EF}$=2.
分析 连接AF,由直角三角形的性质得到BF=CF=AF,根据等腰三角形的性质得到∠B=∠BAF,于是得到∠AFC=2∠B=2α通过三角形全等得到AP=CK,求得CK-CP=AC,根据三角函数的定义得到cosα×EF=$\frac{BF}{BE}$×EF=$\frac{BF×EF}{BE}$,过F作FD⊥AB于D,推出FD=cosα×EF根据三角形的中位线的性质得到DF=$\frac{1}{2}$AC,即可得到结论
解答 解:如图,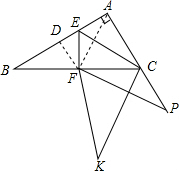
连接AF,
∵EF是BC的垂直平分线,∠BAC=90°,
∴BF=CF=AF,
∴∠B=∠BAF,
∴∠AFC=2∠B=2α,
∴∠AFP=∠KFC,
∵FP=CK,
在△AFP与△CFK中,
$\left\{\begin{array}{l}{AF=FC}\\{∠AFP=∠CFK}\\{FP=FK}\end{array}\right.$
∴△AFP≌△CFK,
∴AP=CK,
∴CK-CP=AC,
过F作FD⊥AB于D,
∴FD=cosα×EF,
∵F是BC的中点,AB⊥AC,
∴DF为△ABC的中位线,
∴DF∥AC,DF=$\frac{1}{2}$AC,
∴$\frac{CK-CP}{cosα×EF}=\frac{AC}{\frac{1}{2}AC}$=2.
故答案为:2.
点评 本题考查了旋转的性质,全等三角形的判定和性质,直角三角形的性质,三角形的中位线的性质,线段垂直平分线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
17.下列说法中正确的是( )
| A. | $\sqrt{4}$是一个无理数 | B. | $\sqrt{81}$的平方根是±3 | ||
| C. | 8的立方根是±2 | D. | 一个数的算术平方根一定是正数 |
12.若关于x的方程$\frac{2}{x-2}$+$\frac{m}{2-x}=1$的解为正数,则m的取值范围是( )
| A. | m<4 | B. | m>4 | C. | m<4且m≠2 | D. | m>0且m≠2 |
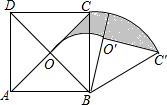 如图,正方形ABCD中,对角线AC、BD相交于点O,△OBC绕点B顺时针旋转60°得到△0′BC′,若AB=2,则图中阴影部分的面积是 $\frac{π}{3}$.
如图,正方形ABCD中,对角线AC、BD相交于点O,△OBC绕点B顺时针旋转60°得到△0′BC′,若AB=2,则图中阴影部分的面积是 $\frac{π}{3}$.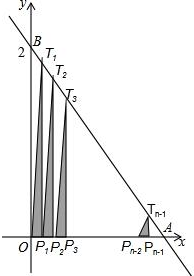 如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n段,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{2015}{4032}$.
如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n段,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{2015}{4032}$.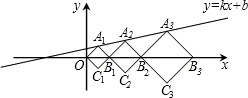 在平面直角坐标系xOy中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2按图中所示的方式放置,点A1、A2、A3…和B1、B2、B3…分别在直线y=kx+b和x轴上,如果A1(1,-1),A2($\frac{7}{2}$,$\frac{3}{2}$),则点A2016的坐标是(5×($\frac{3}{2}$)2015-4,($\frac{3}{2}$)2015).
在平面直角坐标系xOy中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2按图中所示的方式放置,点A1、A2、A3…和B1、B2、B3…分别在直线y=kx+b和x轴上,如果A1(1,-1),A2($\frac{7}{2}$,$\frac{3}{2}$),则点A2016的坐标是(5×($\frac{3}{2}$)2015-4,($\frac{3}{2}$)2015).