题目内容
2.探究规律,在一列数$\sqrt{1}$,$\sqrt{2}$,$\sqrt{3}$,$\sqrt{4}$中,$\sqrt{1}$=1,$\sqrt{4}$=2.在前4个数中,有2个有理数,$\sqrt{1}$,$\sqrt{2}$,$\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$,$\sqrt{6}$,$\sqrt{7}$,$\sqrt{8}$,$\sqrt{9}$中,有3个有理数1,2,3.在这个数列中,要考察里面有多少个有理数,只要观察最后一个被开方数接近于哪个平方数,那么就有这个邻近的完全平方数的算术平方根个有理数.解答:(1)在$\sqrt{1}$,$\sqrt{2}$,$\sqrt{3}$,$\sqrt{4}$,…$\sqrt{2015}$中有多少个有理数?
(2)有多少个无理数?
分析 (1)由于2015最接近的是45×45=2025,依此可得在$\sqrt{1}$,$\sqrt{2}$,$\sqrt{3}$,$\sqrt{4}$,…$\sqrt{2015}$中有多少个有理数;
(2)用这列数的个数减去有理数的个数,即可求出有多少个无理数.
解答 解:(1)2015最接近的是45×45=2025,
所以有45-1=44个有理数;
(2)2015-44=1971(个).
答:有1971个无理数.
点评 考查了实数,本题关键是由2015最接近的是45×45=2025,得到这列数中有理数的个数.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
12.下列式子成立的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | (-$\sqrt{3}$)2=9 | C. | $\sqrt{9}$=±3 | D. | $\root{3}{-8}$=-2 |
17.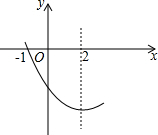 如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )
如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )
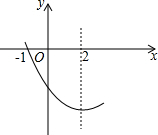 如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )
如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )| A. | ①②③ | B. | ③④⑤ | C. | ②④⑤ | D. | ①③④⑤ |
7.下列运算正确的是( )
| A. | 992=(100-1)2=1002-1 | B. | 3a+2b=5ab | ||
| C. | $\sqrt{9}$=±3 | D. | x7÷x5=x2 |
14.一元一次不等式-3x<12的解集是( )
| A. | x<4 | B. | x>4 | C. | x<-4 | D. | x>-4 |
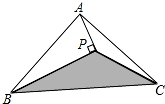 如图,△ABC的面积为1cm2,BP平分∠ABC,AP⊥BP于P,则△PBC的面积为0.5cm2.
如图,△ABC的面积为1cm2,BP平分∠ABC,AP⊥BP于P,则△PBC的面积为0.5cm2.