题目内容
13.如图,A、B为⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合),我们称∠APB为⊙O上关于点A、B的滑动角.已知∠APB是⊙O上关于点A、B的滑动角,(1)若AB为⊙O的直径,则∠APB=90°;
(2)若⊙O半径为1,AB=$\sqrt{2}$,求∠APB的度数;
(3)若⊙O半径为1,AB=$\sqrt{2}$,AC=$\sqrt{3}$,求∠BAC的度数.

分析 (1)由AB为⊙O的直径,根据直径所对的圆周角是直角,即可求得答案;
(2)由⊙O半径为1,AB=$\sqrt{2}$,可求得∠AOB的度数,又由圆周角定理即可求得∠APB的度数;
(3)根据题意画出图形,作出辅助线,由于AC与AB在圆心的同侧还是异侧不能确定,故应分两种情况进行讨论.
解答  解:(1)∵AB为⊙O的直径,
解:(1)∵AB为⊙O的直径,
∴∠APB=90°.
故答案为:90°;
(2)连接OA,OB,AB,
∵⊙O半径为1,AB=$\sqrt{2}$,
∴OA=OB=1,AB=$\sqrt{2}$,
∴OA2+OB2=AB2,
∴∠AOB=90°,
∴当点P在优弧AB上时,∠APB=$\frac{1}{2}$∠AOB=45°,
当点P在劣弧AB上时,∠APB=180°-45°=135°,
∴∠APB的度数为:45°或135°;
(3)解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,
∴AE=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$,AD=$\frac{1}{2}$AB=$\frac{\sqrt{2}}{2}$,
∴sin∠AOE=$\frac{AE}{AO}$=$\frac{\sqrt{3}}{2}$,sin∠AOD=$\frac{AD}{AO}$=$\frac{\sqrt{2}}{2}$,
∴∠AOE=60°,∠AOD=45°,
∴∠BAO=45°,∠CAO=90°-60°=30°,
∴∠BAC=45°+30°=75°,或∠BAC′=45°-30°=15°.
∴∠BAC=15°或75°.
点评 本题考查了圆周角定理、垂径定理及直角三角形的性质.注意掌握辅助线的作法是解此题的关键.

练习册系列答案
相关题目
1.已知∠AOB=50°,∠BOC=30°,OD平分∠AOC,则∠AOD的度数为( )
| A. | 20° | B. | 80° | C. | 20°或80° | D. | 10°或40° |
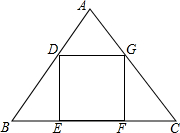 如图,在△ABC中,AB=AC,正方形DEFG的顶点D、G分别在AB、AC上,EF在BC上,设AB=5,BC=6,求正方形DEFG的边长.
如图,在△ABC中,AB=AC,正方形DEFG的顶点D、G分别在AB、AC上,EF在BC上,设AB=5,BC=6,求正方形DEFG的边长. 如图所示,在矩形ABCD的顶点A处拴了一只小羊,在B、C、D处各有一筐青草,要使小羊至少能吃到一筐子里的草.如果AB=5,BC=12,则拴羊绳的长l最少是5.
如图所示,在矩形ABCD的顶点A处拴了一只小羊,在B、C、D处各有一筐青草,要使小羊至少能吃到一筐子里的草.如果AB=5,BC=12,则拴羊绳的长l最少是5.