题目内容
3.如图是单位长度是1的网格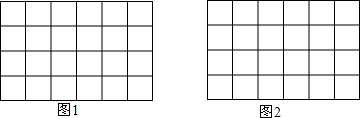
(1)在图1中画出一条边长为$\sqrt{5}$的线段;
(2)在图2中画出一个以格点为顶点,三边长都为无理数的直角三角形.
分析 (1)由勾股定理得出$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,画出线段即可;
(2)画一个边长$\sqrt{2}$、2$\sqrt{2}$、$\sqrt{10}$的三角形即可.
解答 解: (1)由勾股定理得:$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
(1)由勾股定理得:$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
线段AB即为所求,
如图1所示:
(2)由勾股定理得:
$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,$\sqrt{{2}^{2}+{2}^{2}}$=$2\sqrt{2}$,$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,;
∵($\sqrt{2}$)2+(2$\sqrt{2}$)2=($\sqrt{10}$)2,
∴以边长$\sqrt{2}$、2$\sqrt{2}$、$\sqrt{10}$的三角形为直角三角形,
如图2所示.
点评 本题考查了勾股定理、正方形的性质、勾股定理的逆定理;熟练掌握勾股定理和勾股定理的逆定理,并能进行计算与作图是解决问题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
11.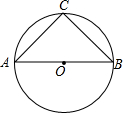 若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
 若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
8. 如图,AB=AC,下列条件不一定能证明△ABD≌△ACE的是( )
如图,AB=AC,下列条件不一定能证明△ABD≌△ACE的是( )
 如图,AB=AC,下列条件不一定能证明△ABD≌△ACE的是( )
如图,AB=AC,下列条件不一定能证明△ABD≌△ACE的是( )| A. | ∠B=∠C | B. | AE=AD | C. | BE=DC | D. | BD=CE |
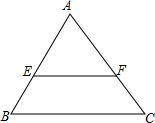 如图,△ABC中,EF∥BC,且EF=$\frac{2}{3}$BC=4cm,△AEF的周长为10cm,求BCFE的周长.
如图,△ABC中,EF∥BC,且EF=$\frac{2}{3}$BC=4cm,△AEF的周长为10cm,求BCFE的周长.