题目内容
7. 如图,已知AB∥CD,EF∥MN,∠1=115°.
如图,已知AB∥CD,EF∥MN,∠1=115°.(1)求∠2和∠4的度数;
(2)本题隐含着一个规律,请你根据(1)的结果进行归纳:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的2倍少60°,求这两个角的度数.
分析 (1)由平行线的性质可求得∠2,再求得∠4;
(2)由(1)的结果可得到这两个角相等或互补;
(3)根据(2)的规律可知这两个角互补或相等,利用方程可求得这两个角.
解答 解:(1)∵AB∥CD,
∴∠2=∠1=115°,
∵EF∥MN,
∴∠4+∠2=180°,
∴∠4=180°-∠2=65°;
(2)由(1)可知如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补,
故答案为:相等或互补;
(3)由(2)可知这两个角互补或相等,设一个角为x°,则另一个角为2x°-60°,
根据两个角互补可得,x+2x-60=180,
解得x=80,
∴这两个角分别为80°和100°.
根据两个角相等可得,x=2x-60,
解得x=60,
∴这两个角分别为60°和60°.
点评 本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,解题时注意:①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
2.下列方程中,没有实数根的是( )
| A. | 2x+3=0 | B. | x2-1=0 | C. | $\frac{1}{x-2}$=$\frac{1-x}{2-x}$-3 | D. | x2+x-1=0 |
17. 为了治理大气污染,某城市抽取了该地区一年中某些天的空气质量指数,绘制了如下的统计图表:
为了治理大气污染,某城市抽取了该地区一年中某些天的空气质量指数,绘制了如下的统计图表:
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a=6,m=50;
(2)“轻度污染”所对应扇形的圆心角是72度;
(3)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前统计,请你估计一年(365天)该市有多少天不适宜开展户外活动.(结果保留整数)
 为了治理大气污染,某城市抽取了该地区一年中某些天的空气质量指数,绘制了如下的统计图表:
为了治理大气污染,某城市抽取了该地区一年中某些天的空气质量指数,绘制了如下的统计图表:| 级别 | 指数 | 天数 |
| 1级:优 | 0-50 | 3 |
| 2级:良 | 51-100 | 24 |
| 3级:轻度污染 | 101-200 | 10 |
| 度污染 | 201-300 | 7 |
| 5级:重度污染 | 大于300 | a |
| 合计 | m |
(1)空气质量指数统计表中的a=6,m=50;
(2)“轻度污染”所对应扇形的圆心角是72度;
(3)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前统计,请你估计一年(365天)该市有多少天不适宜开展户外活动.(结果保留整数)
 如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求A,B两点间的距离(结果精确到0.1km).
如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求A,B两点间的距离(结果精确到0.1km).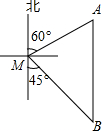 如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.
如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.