题目内容
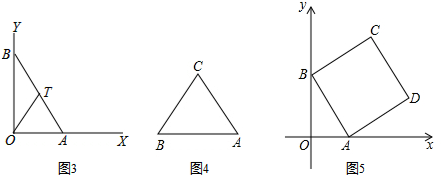
已知一个正方形ABCD的边长为a,分别在边AB,BC,CD,DA上截取相等的线段AP,BQ,CR,DS,连接PQ,QR,RS,SP,则得正方形PQRS,问要使正方形PQRS的面积最小,所截取的四条线段每条应该多长?
考点:二次函数的应用
专题:
分析:根据题意画出图形,进而得出S与x的函数关系,即可得出答案.
解答: 解:如图所示:设AP=x,则BQ=CR=DS=x,则BP=CQ=DR=SA=a-x,
解:如图所示:设AP=x,则BQ=CR=DS=x,则BP=CQ=DR=SA=a-x,
故正方形PQRS的面积=正方形ABCD的面积-4S△APS=a2-4×
x(a-x)=2x2-2ax+a2,
当x=-
=
时,
正方形PQRS的面积最小,
此时a-x=a-
=
,
即当取正方形ABCD各边中点时,PQRS面积最小.
 解:如图所示:设AP=x,则BQ=CR=DS=x,则BP=CQ=DR=SA=a-x,
解:如图所示:设AP=x,则BQ=CR=DS=x,则BP=CQ=DR=SA=a-x,故正方形PQRS的面积=正方形ABCD的面积-4S△APS=a2-4×
| 1 |
| 2 |
当x=-
| 2a |
| 2×2 |
| a |
| 2 |
正方形PQRS的面积最小,
此时a-x=a-
| a |
| 2 |
| a |
| 2 |
即当取正方形ABCD各边中点时,PQRS面积最小.
点评:此题主要考查了二次函数的应用,得出函数关系式是解题关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知一次函数y=x+m的图象经过一、三、四象限,则m的值可以是( )
| A、-2 | B、1 | C、0 | D、2 |
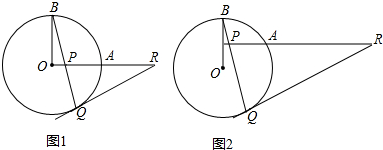
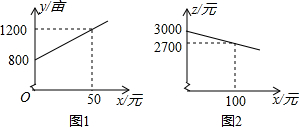 某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系. (1)如图1、图2,点P是⊙O外一点,作直线OP,交⊙O于点M、N,则有结论:①点M是点P到⊙O的最近点;②点N是点P到⊙O的最远点.
(1)如图1、图2,点P是⊙O外一点,作直线OP,交⊙O于点M、N,则有结论:①点M是点P到⊙O的最近点;②点N是点P到⊙O的最远点.