题目内容
6．无论k为何值，一次函数（2k-1）x-（k-3）y-（k-13）=0的图象必经过定点（-2，-5）．分析 将原方程转化为（2x-y-1）k+（13-x+3y）=0，令2x-y-1=0①且13-x+3y=0②；然后根据①②求出该定点即可．
解答 解：由（2k-1）x-（k-3）y-（k-13）=0，得
即（2x-y-1）k+（13-x+3y）=0，
∴2x-y-1=0，①
且13-x-3y=0，②
∴一次函数（2k-1）x-（k-3）y-（k-13）=0的图象就和k无关，恒过一定点．
由①②，解之得：x=-2 y=-5 所以过定点（-2，-5）；
故答案为：（-2，-5）
点评 本题考查了一次函数图象上点的坐标特征，关键是将原方程转化为（2x-y-1）k+（13-x+3y）=0．
练习册系列答案
相关题目
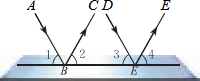如图，一束平行光线AB与DE射向一个水平镜面而后被反射，此时∠1=∠2，∠3=∠4．反射光线BC与EF也平行吗？说明理由．
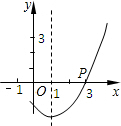已知二次函数y=ax2+bx+c的图象如图所示，有以下结论：
11．点（1，-2）在抛物线y=x2-5xsinα+1上，且α为锐角，则cosα等于（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{12}{13}$ | D． | $\frac{5}{13}$ |
如图，已知菱形ABCD的边长为2，∠A=45°，将菱形ABCD绕点A旋转45°，得到菱形AB1C1D1，其中B、C、D的对应点分别是B1、C1、D1，那么点C、C1的距离为2$\sqrt{2}$．