题目内容
2．计算（1）$\frac{1}{a-1}$-$\frac{a}{a-1}$
（2）$\frac{{a}^{2}}{{a}^{2}+2a}$-（$\frac{{a}^{2}}{a-2}$-$\frac{4}{a-2}$）
（3）$\frac{{a}^{2}+1}{a-1}$-a+1．
分析 （1）原式利用同分母分式的减法法则计算，约分即可得到结果；
（2）原式括号中利用同分母分式的减法法则计算，约分后两项通分并利用同分母分式的减法法则计算即可得到结果；
（3）原式通分并利用同分母分式的减法法则计算即可得到结果．
解答 解：（1）原式=$\frac{1-a}{a-1}$=$\frac{-（a-1）}{a-1}$=-1；
（2）原式=$\frac{{a}^{2}}{a（a+2）}$-$\frac{（a+2）（a-2）}{a-2}$=$\frac{a}{a+2}$-a-2=$\frac{a-（a+2）^{2}}{a+2}$；
（3）原式=$\frac{{a}^{2}+1-（a-1）^{2}}{a-1}$=$\frac{2a}{a-1}$．
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
14．直线y=2x+2沿y轴向下平移6个单位后与x轴的交点坐标是（ ）
| A． | （-4，0） | B． | （-1，0） | C． | （0，2） | D． | （2，0） |
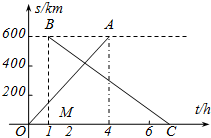甲、乙两城市之间开通了动车组高速列车．已知每隔2h有一列速度相同的动车组列车从甲城开往乙城．如图，OA是第一列动车组列车离开甲城的路程s（km）与运行时间t（h）的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s（km）与运行时间t（h）的函数图象．请根据图中的信息，解答下列问题：
10．直线y=ax+b经过第二、三、四象限，则下列结论正确的是（ ）
| A． | $\sqrt{（a+b）^{2}}$=a+b | |
| B． | 点（a，b）在第一象限 | |
| C． | 抛物线y=ax2+bx+c的对称轴经过第二、三象限 | |
| D． | 反比例函数y=$\frac{a}{x}$，当x＞0时，函数值随x的增大而减小 |
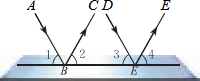如图，一束平行光线AB与DE射向一个水平镜面而后被反射，此时∠1=∠2，∠3=∠4．反射光线BC与EF也平行吗？说明理由．
11．点（1，-2）在抛物线y=x2-5xsinα+1上，且α为锐角，则cosα等于（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{12}{13}$ | D． | $\frac{5}{13}$ |