题目内容
2.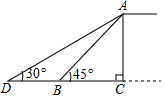 某市为缓解城市交通压力,决定修建人行天桥.原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°.求BD的长.(结果保留根号).
某市为缓解城市交通压力,决定修建人行天桥.原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°.求BD的长.(结果保留根号).
分析 先在Rt△ABC中利用45°的三角函数可计算出AC,再在Rt△ADC中利用∠D的正切值可求出CD的长,然后计算CD-BC即可.
解答 解:在Rt△ABC中,AB=6m,∠ABC=45°,
∴AC=BC=AB•tan45°=6×$\frac{\sqrt{2}}{2}$=3 $\sqrt{2}$,
在Rt△ADC中,∵tanD=$\frac{AC}{CD}$,
∴CD=$\frac{AC}{tan30°}$═3$\sqrt{2}$÷$\frac{\sqrt{3}}{3}$=3$\sqrt{6}$,
∴BD=CD-BC=3$\sqrt{6}$-3 $\sqrt{2}$.
答:BD的长为(3 $\sqrt{6}$-3$\sqrt{2}$) m.
点评 本题考查了解直角三角形的应用:将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.

练习册系列答案
相关题目
12.算式(-20)-(+3)-(+5)-(-7)写成省略加号的和的形式正确的为( )
| A. | 20+3+5-7 | B. | -20-3-5-7 | C. | -20-3+5+7 | D. | -20-3-5+7 |
13. 如图所示的圆柱,从左边看是( )
如图所示的圆柱,从左边看是( )
 如图所示的圆柱,从左边看是( )
如图所示的圆柱,从左边看是( )| A. |  | B. |  | C. |  | D. |  |
10.下列函数中,自变量x的取值范围为x>3的是( )
| A. | y=$\frac{1}{x-3}$ | B. | y=$\frac{1}{\sqrt{x-3}}$ | C. | y=x-3 | D. | y=$\sqrt{x-3}$ |
 如图,已知点E,F,G,H分别是正方形ABCD四条边上的点,并且AE=BF=CG=DH.求证:四边形EFGH是正方形.
如图,已知点E,F,G,H分别是正方形ABCD四条边上的点,并且AE=BF=CG=DH.求证:四边形EFGH是正方形.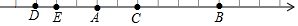 如下图,数轴上相邻刻度之间的距离是$\frac{1}{5}$,点A表示的数是$-\frac{4}{5}$,又知点B和点C表示的数互为相反数,则点E表示的有理数是-$\frac{6}{5}$,点D与点C之间相距1.
如下图,数轴上相邻刻度之间的距离是$\frac{1}{5}$,点A表示的数是$-\frac{4}{5}$,又知点B和点C表示的数互为相反数,则点E表示的有理数是-$\frac{6}{5}$,点D与点C之间相距1. 如图所示,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为$\frac{1}{{{2^{2012}}}}$.
如图所示,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为$\frac{1}{{{2^{2012}}}}$.