题目内容
17.在函数y=$\frac{\sqrt{4x-3}}{x-2}$中,自变量x的取值范围是x≥$\frac{3}{4}$且x≠2.分析 根据被开方数大于等于0,分母不等于0列式计算即可得解.
解答 解:由题意得,4x-3≥0且x-2≠0,
解得x≥$\frac{3}{4}$且x≠2.
故答案为:x≥$\frac{3}{4}$且x≠2.
点评 本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
12.如表是二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y的对应关系,一元二次方程ax2+bx+c=$\frac{3}{10}$(a≠0)的一个解x的取值范围是6.2<x<6.3.
| x | 6.1 | 6.2 | 6.3 | 6.4 |
| y=ax2+bx+c | -0.3 | -0.1 | 0.2 | 0.4 |
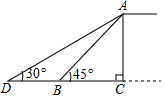 某市为缓解城市交通压力,决定修建人行天桥.原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°.求BD的长.(结果保留根号).
某市为缓解城市交通压力,决定修建人行天桥.原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°.求BD的长.(结果保留根号). 如图:A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=2,且MN=4,P为直线上的动点,|PA-PB|的最大值为2$\sqrt{5}$.
如图:A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=2,且MN=4,P为直线上的动点,|PA-PB|的最大值为2$\sqrt{5}$.