题目内容
12. 如图所示,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为$\frac{1}{{{2^{2012}}}}$.
如图所示,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为$\frac{1}{{{2^{2012}}}}$.
分析 根据题意可知第2个正方形的边长是 $\frac{\sqrt{2}}{2}$×2,则第3个正方形的边长是( $\frac{\sqrt{2}}{2}$)2×2,…,进而可找出规律,第n个正方形的边长是( $\frac{\sqrt{2}}{2}$)n-1×2,那么易求S2015的值.
解答 解:根据题意:第一个正方形的边长为2;
第二个正方形的边长为:$\frac{\sqrt{2}}{2}$×2;
第三个正方形的边长为:( $\frac{\sqrt{2}}{2}$)2×2,
…
第n个正方形的边长是( $\frac{\sqrt{2}}{2}$)n-1×2,
所以S2015的值是( $\frac{1}{2}$)2012即$\frac{1}{{2}^{2012}}$.
故答案为$\frac{1}{{2}^{2012}}$.
点评 本题考查了正方形的性质、等腰直角三角形的性质、勾股定理.解题的关键是长特殊到一般,探究规律后,应用规律解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
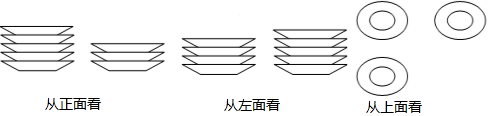
(2)分别从正面、左面、上面三个方向看这些碟子,看到的形状图如图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
| 碟子的个数 | 1 | 2 | 3 | 4 | … |
| 碟子的高度(单位:cm) | 2 | 2+1.5 | 2+3 | 2+4.5 | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从正面、左面、上面三个方向看这些碟子,看到的形状图如图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
1.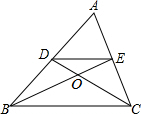 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( )
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( )
 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( )
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
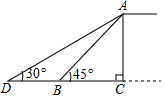 某市为缓解城市交通压力,决定修建人行天桥.原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°.求BD的长.(结果保留根号).
某市为缓解城市交通压力,决定修建人行天桥.原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°.求BD的长.(结果保留根号). 一个长为3,宽为2的长方形从表示-1的点开始绕着数轴无滑动的逆时针滚动一周到达E点,则E点所表示的数是-3.
一个长为3,宽为2的长方形从表示-1的点开始绕着数轴无滑动的逆时针滚动一周到达E点,则E点所表示的数是-3.
 如图:A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=2,且MN=4,P为直线上的动点,|PA-PB|的最大值为2$\sqrt{5}$.
如图:A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=2,且MN=4,P为直线上的动点,|PA-PB|的最大值为2$\sqrt{5}$.