题目内容
用同样规格黑白两色的正方形瓷砖铺设矩形地面,观察下列图形,并解答有关问题:

(1)在第n个图形中,每一个横行共有 块瓷砖,每一竖列共有 块瓷砖,共有 块黑瓷砖.(均用含n的式子表示)
(2)按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求n的值.
(3)是否存在黑瓷砖与白瓷砖块数相等的可能?请计算说明.

(1)在第n个图形中,每一个横行共有
(2)按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求n的值.
(3)是否存在黑瓷砖与白瓷砖块数相等的可能?请计算说明.
考点:一元二次方程的应用,规律型:图形的变化类
专题:
分析:(1)根据每行瓷砖数量得出规律,即可得出答案;
(2)根据题意可得(n+2)(n+3)=506,解关于n的一元二次方程即可;
(3)第一个图形中白色瓷块有1×2=2,黑色瓷块=2×5=10,
第二个图形中白色瓷块有2×3=6,黑色瓷块=2×7=14,
第三个图形中白色瓷块有3×4=12,黑色瓷块=2×9=18…
那么依此类推第n个图形中有白色瓷块=n(n+1),黑色瓷块=2(2n+3),根据题意可得n(n+1)=2(2n+3),解关于n的方程即可.
(2)根据题意可得(n+2)(n+3)=506,解关于n的一元二次方程即可;
(3)第一个图形中白色瓷块有1×2=2,黑色瓷块=2×5=10,
第二个图形中白色瓷块有2×3=6,黑色瓷块=2×7=14,
第三个图形中白色瓷块有3×4=12,黑色瓷块=2×9=18…
那么依此类推第n个图形中有白色瓷块=n(n+1),黑色瓷块=2(2n+3),根据题意可得n(n+1)=2(2n+3),解关于n的方程即可.
解答:解:(1)在第n个图形中,每一个横行共有n+3块瓷砖,每一竖列共有n+6块瓷砖,共有4n+6块黑瓷砖.
故答案为:n+3,n+2,4n+6;
(2)根据题意得:n2+5n+6=506,
解得n1=20,n2=-25(不符合题意,舍去);
(3)根据题意得:n(n+1)=2(2n+3),
解得n=
(不符合题意,舍去),
∴不存在黑瓷砖与白瓷砖块数相等的情形.
故答案为:n+3,n+2,4n+6;
(2)根据题意得:n2+5n+6=506,
解得n1=20,n2=-25(不符合题意,舍去);
(3)根据题意得:n(n+1)=2(2n+3),
解得n=
3±
| ||
| 2 |
∴不存在黑瓷砖与白瓷砖块数相等的情形.
点评:本题考查了一元二次方程的应用,解题的关键主要是寻找规律,还使用了解一元二次方程的知识.

练习册系列答案
相关题目
下列数组中,不是勾股数的是( )
| A、3、4、5 |
| B、9、12、15 |
| C、7、24、25 |
| D、12、18、22 |
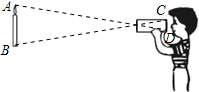 如图,小强自制了一个小孔成像装置,其中纸筒的长度为15cm,他准备了一支长为20cm的蜡烛,想要得到高度为4cm的像,蜡烛与纸筒的距离应该为( )
如图,小强自制了一个小孔成像装置,其中纸筒的长度为15cm,他准备了一支长为20cm的蜡烛,想要得到高度为4cm的像,蜡烛与纸筒的距离应该为( )| A、60cm | B、65cm |
| C、70cm | D、75cm |
下列长度的四根木棒,能与3cm,7cm长的两根木棒钉成一个三角形的是( )
| A、3cm | B、4cm |
| C、6cm | D、10cm |
下列各数中,无理数是( )
| A、3.14 | ||
B、
| ||
C、
| ||
D、
|