题目内容
某油箱有60L油,油从管道中均匀流出一小时即可流完,则油箱中所剩的油Q(升)与流出的时间t(分)之间的函数关系式为 ,自变量t的取值范围 .
考点:函数关系式,函数自变量的取值范围
专题:
分析:应先得到1分钟的流油量;油箱中剩油量=原来有的油量-t分流的油量.
解答:解:∵1小时也就是60分钟可流完60L油,
∴1分钟可流油60÷60=1L,
∴t分流的油量t,
∴Q=60-t,
∵油箱中剩余油量Q≥0,即:60-t≥0,解得:0≤t≤60,
故答案为:Q=60-t,0≤t≤60.
∴1分钟可流油60÷60=1L,
∴t分流的油量t,
∴Q=60-t,
∵油箱中剩余油量Q≥0,即:60-t≥0,解得:0≤t≤60,
故答案为:Q=60-t,0≤t≤60.
点评:本题考查了函数关系式及函数自变量的取值范围,属于基础题,得到油箱中剩油量的等量关系是解决本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
正比例函数y=x与反比例函数y=-
的图象大致是( )
| 2 |
| x |
A、 |
B、 |
C、 |
D、 |
 如图:直线y=-
如图:直线y=- 如图,某山坡AB的坡角∠BAC=30°,则该山坡AB的坡度为
如图,某山坡AB的坡角∠BAC=30°,则该山坡AB的坡度为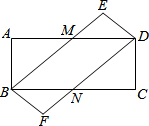 如图,在矩形ABCD和矩形BFDE中,AD与BE交于点M,BC与DF交于点N.
如图,在矩形ABCD和矩形BFDE中,AD与BE交于点M,BC与DF交于点N.