题目内容
 如图,△ABC中,∠C=60°,剪去这个60°角后,得到一个四边形,那么∠BDE+∠AED的度数为( )
如图,△ABC中,∠C=60°,剪去这个60°角后,得到一个四边形,那么∠BDE+∠AED的度数为( )| A、180° | B、240° |
| C、120° | D、300° |
考点:多边形内角与外角,三角形内角和定理
专题:计算题
分析:三角形纸片中,剪去其中一个60°的角后变成四边形,则根据多边形的内角和等于360度即可求得∠BDE+∠AED的度数.
解答:解:根据三角形的内角和定理得:
四边形除去∠BDE,∠AED后的两角的度数为180°-60°=120°,
则根据四边形的内角和定理得:
∠BDE+∠AED=360°-120°=240°.
故选B.
四边形除去∠BDE,∠AED后的两角的度数为180°-60°=120°,
则根据四边形的内角和定理得:
∠BDE+∠AED=360°-120°=240°.
故选B.
点评:主要考查了三角形及四边形的内角和是360度的实际运用与三角形内角和180度之间的关系.

练习册系列答案
相关题目
计算
3的结果为( )
| (xy) |
| xy3 |
| A、y2 |
| B、x2 |
| C、1 |
| D、y-2 |
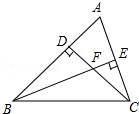 已知:如图,△ABC中,∠ABC=45°,AC=4cm,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点F.则BF=( )
已知:如图,△ABC中,∠ABC=45°,AC=4cm,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点F.则BF=( )| A、4cm | B、3cm |
| C、2cm | D、1cm |
 如图,已知∠B=∠EFD,BF=CE,添加下列一个条件,不能使△ABC≌△DEF的是( )
如图,已知∠B=∠EFD,BF=CE,添加下列一个条件,不能使△ABC≌△DEF的是( )| A、∠A=∠D |
| B、∠ACB=∠E |
| C、AB=DF |
| D、AC=DE |
 已知不等①、②、③的解集在数轴上的表示如图,则它们的公共部分的解集是( )
已知不等①、②、③的解集在数轴上的表示如图,则它们的公共部分的解集是( )| A、-1≤x<3 | B、1≤x<3 |
| C、-1≤x<1 | D、无解 |
已知△ABC中,∠A=2∠B=3∠C,则△ABC为( )
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、无法确定 |
 如图,已知BD,CE分别是△ABC的外角平分线,过点A分别作BD,CE的垂线,交BD,CE于点F,G,交直线BC于点M,N.求证:FG∥MN,FG=
如图,已知BD,CE分别是△ABC的外角平分线,过点A分别作BD,CE的垂线,交BD,CE于点F,G,交直线BC于点M,N.求证:FG∥MN,FG= 如图,在7×8的方格纸中,已知图中每个小正方形的边长都为1,求图中阴影部分的面积.
如图,在7×8的方格纸中,已知图中每个小正方形的边长都为1,求图中阴影部分的面积.