题目内容
6.观察不等式:32-12=8×1,52-32=8×2,72-52=8×3,92-72=8×4…(1)用含有字母n(n≥1的整数)的等式表示这一规律;
(2)请用所学知识验证这个规律的正确性;
(3)借助你发现的规律把400写成两个正整数的平方差的形式:400=(101)2-(99)2.
分析 (1)通过观察可发现两个连续奇数的平方差是8的倍数,第n个等式为:(2n+1)2-(2n-1)2=8n;
(2)根据平方差公式即可求解;
(3)根据发现的规律计算即可.
解答 解:(1)用含有字母n(n≥1的整数)的等式表示这一规律:(2n+1)2-(2n-1)2=8n(n≥1的整数);
(2)(2n+1)2-(2n-1)2
=(2n+1+2n-1)(2n+1-2n+1)
=4n×2
=8n;
(3)400=8×50=(2×50+1)2-(2×50-1)2=1012-992.
故答案为:101,99.
点评 此题考查了数字的变化类,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力,本题的关键规律是:(2n+1)2-(2n-1)2=8n.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
7. 如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )
如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )
 如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )
如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
 如图,长方形ABCD是由k个相同的长方形组成,上下各有4个水平放置的长方形,中间竖放若干个长方形,并且宽AB是长AD的$\frac{7}{12}$,则k的值为14.
如图,长方形ABCD是由k个相同的长方形组成,上下各有4个水平放置的长方形,中间竖放若干个长方形,并且宽AB是长AD的$\frac{7}{12}$,则k的值为14.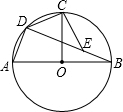 已知AB是⊙O的直径,半径OC⊥AB,D为$\widehat{AC}$上任意一点,E为弦BD上一点,且 BE=AD.
已知AB是⊙O的直径,半径OC⊥AB,D为$\widehat{AC}$上任意一点,E为弦BD上一点,且 BE=AD. 如图,两张48×40的长方形纸片有一个顶点重合,重叠放置的尺寸如图所标示,则图中阴影部分的面积=984.
如图,两张48×40的长方形纸片有一个顶点重合,重叠放置的尺寸如图所标示,则图中阴影部分的面积=984. 在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.求证下列结论:
在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.求证下列结论: 有一个数值转换机,原理如图所示,若开始输入的x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,…依次继续下去
有一个数值转换机,原理如图所示,若开始输入的x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,…依次继续下去 如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).点D在线段PQ上,且PD=PC.
如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).点D在线段PQ上,且PD=PC.