题目内容
19.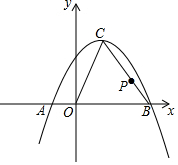 已知:如图,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).
已知:如图,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).(1)试确定该抛物线的函数表达式;
(2)已知点C是该抛物线的顶点,求△OBC的面积;
(3)若点P是线段BC上的一动点,求OP的最小值.
分析 (1)将点A和点B的坐标代入抛物线的解析式得到关于a、c的方程组,从而可求得a、c的值,故此可得到抛物线的解析式;
(2)先利用配方法求抛物线的顶点C的坐标,然后依据三角形的面积公式求解即可;
(3)根据垂线段最短可知,当OP⊥BC,即OP是BC边上的高时,OP的值最小.利用两点间的距离公式求出BC,再根据三角形的面积公式求出OP即可.
解答 解:(1)∵抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0),
∴$\left\{\begin{array}{l}{a-1+c=0}\\{9a+3+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=\frac{3}{2}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+x+$\frac{3}{2}$.
(2)∵y=-$\frac{1}{2}$x2+x+$\frac{3}{2}$=-$\frac{1}{2}$(x-1)2+2,
∴抛物线的顶点C的坐标为(1,2),
∴S△OBC=$\frac{1}{2}$×3×2=3;
(3)当OP是BC边上的高时,OP的值最小.
∵B(3,0),C(1,2),
∴BC=$\sqrt{(1-3)^{2}+(2-0)^{2}}$=2$\sqrt{2}$.
∵S△OBC=$\frac{1}{2}$BC•OP=3,
∴OP=$\frac{6}{BC}$=$\frac{3\sqrt{2}}{2}$,
即OP的最小值是$\frac{3\sqrt{2}}{2}$.
点评 本题考查了抛物线与x轴的交点,待定系数法求二次函数解析式,二次函数的性质,三角形的面积,垂线的性质,两点间的距离公式等知识,正确求出抛物线的解析式是解题的关键.

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案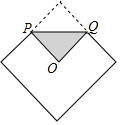 将边长为1的正方形巾的一角折叠至正方形的中心位置,折痕PQ的长为( )
将边长为1的正方形巾的一角折叠至正方形的中心位置,折痕PQ的长为( )| A. | 1 | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
(1)16的平方根是±4
(2)若x=3,则x2-3x=0
(3)六边形的内角和是外角和的2倍
(4)顺次连接菱形四边中点的线段组成的四边形是矩形
其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 有一个外包装盒为正六棱柱体(如图),它的左视图是( )
有一个外包装盒为正六棱柱体(如图),它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
请回答下列问题:
| 时间 | 第一天7:00-8:00 | 第二天7:00-8:00 | 第三天7:00-8:00 | 第四天7:00-8:00 | 第五天7:00-8:00 |
| 需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(2)由随机抽样估计,平均每天在7:00-8:00需要租用公共自行车的人数是多少?
 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A. | ∠1和∠2是内错角 | B. | ∠1和∠5是同位角 | ||
| C. | ∠1和∠2是同旁内角 | D. | ∠1和∠4是内错角 |
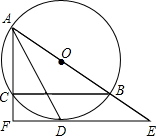 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF.