题目内容
11.已知矩形ABCD的四个顶点均在反比例函数y=$\frac{1}{x}$的图象上,且点A的横坐标是2,则矩形ABCD的面积为$\frac{15}{2}$.分析 先根据点A在反比例函数y=$\frac{1}{x}$的图象上,且点A的横坐标是2,可得A(2,$\frac{1}{2}$),再根据B($\frac{1}{2}$,2),D(-$\frac{1}{2}$,-2),运用两点间距离公式求得AB和AD的长,即可得到矩形ABCD的面积.
解答 解:如图所示,根据点A在反比例函数y=$\frac{1}{x}$的图象上,且点A的横坐标是2,可得A(2,$\frac{1}{2}$),
根据矩形和双曲线的对称性可得,B($\frac{1}{2}$,2),D(-$\frac{1}{2}$,-2),
由两点间距离公式可得,AB=$\sqrt{(2-\frac{1}{2})^{2}+(\frac{1}{2}-2)^{2}}$=$\frac{3}{2}\sqrt{2}$,AD=$\sqrt{(2+\frac{1}{2})^{2}+(\frac{1}{2}+2)^{2}}$=$\frac{5}{2}\sqrt{2}$,
∴矩形ABCD的面积=AB×AD=$\frac{3}{2}\sqrt{2}$×$\frac{5}{2}\sqrt{2}$=$\frac{15}{2}$,
故答案为:$\frac{15}{2}$.
点评 本题主要考查了反比例函数图象上点的坐标特征以及矩形的性质的综合应用,解决问题的关键是画出图形,依据两点间距离公式求得矩形的边长.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
1.2016年山东省高考报名人数位居全国第三,约有696000人报名,将696000用科学记数法表示为( )
| A. | 69.6×104 | B. | 6.96×105 | C. | 6.96×106 | D. | 0.696×106 |
2.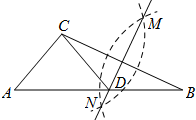 如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
 如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )| A. | ∠CAD=40° | B. | ∠ACD=70° | C. | 点D为△ABC的外心 | D. | ∠ACB=90° |
6.下列给出的函数中,其图象是中心对称图形的是( )
①函数y=x;②函数y=x2;③函数y=$\frac{1}{x}$.
①函数y=x;②函数y=x2;③函数y=$\frac{1}{x}$.
| A. | ①② | B. | ②③ | C. | ①③ | D. | 都不是 |
16.矩形的长与宽分别为a、b,下列数据能构成黄金矩形的是( )
| A. | a=4,b=$\sqrt{5}$+2 | B. | a=4,b=$\sqrt{5}$-2 | C. | a=2,b=$\sqrt{5}$+1 | D. | a=2,b=$\sqrt{5}$-1 |
3.7的相反数是( )
| A. | 7 | B. | -7 | C. | $\frac{1}{7}$ | D. | -$\frac{1}{7}$ |
20. 如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
 如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
如图,∠ACD=120°,∠B=20°,则∠A的度数是( )| A. | 120° | B. | 90° | C. | 100° | D. | 30° |
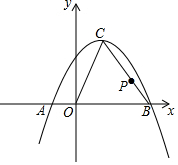 已知:如图,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).
已知:如图,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).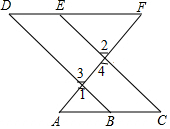 如图,点B在AC上,点E、D、F三点共线,∠2=∠1,∠FEC=∠DBA,把证明AC∥DF的过程补充完整.
如图,点B在AC上,点E、D、F三点共线,∠2=∠1,∠FEC=∠DBA,把证明AC∥DF的过程补充完整.