题目内容
10.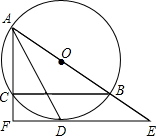 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF.(1)求证:EF是⊙O的切线;
(2)小强同学通过探究发现:AF+CF=2AO,请你帮助小强同学证明这一结论.
分析 (1)连接OD,如图,利用平行线的判定证明OD∥AF,加上AF⊥EF,则OD⊥EF,于是根据切线的判定定理可判断EF是⊙O的切线;
(2)连接CD、BD,作DH⊥AB于H,如图,先利用角平分线的性质得到DF=DH,再证明Rt△ADF≌△ADH得到AF=AH,证明Rt△DCF≌Rt△DBH得到CF=BH,所以AF+CF=AH+BH=AB=2OA.
解答 证明:(1)连接OD,如图,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠BAC,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴OD∥AF,
而AF⊥EF,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)连接CD、BD,作DH⊥AB于H,如图,
∵AD平分∠BAC,DF⊥AF,DH⊥AB,
∴DF=DH,
在Rt△ADF和△ADH中
$\left\{\begin{array}{l}{AD=AD}\\{DF=DH}\end{array}\right.$,
∴Rt△ADF≌△ADH,
∴AF=AH,
∵∠BAD=∠DAC,
∴$\widehat{CD}$=$\widehat{BD}$,
∴CD=BD,
在Rt△DCF和Rt△DBH中
$\left\{\begin{array}{l}{DC=DB}\\{DF=DH}\end{array}\right.$,
∴Rt△DCF≌Rt△DBH,
∴CF=BH,
∴AF+CF=AH+BH=AB=2OA.
点评 本题考查了切线的判定与性质:经过半径的外端且垂直于这条半径的直线是圆的切线.判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;有切线时,常常“遇到切点连圆心得半径”.也考查了圆周角定理和全等三角形的判定与性质.

练习册系列答案
相关题目
1.2016年山东省高考报名人数位居全国第三,约有696000人报名,将696000用科学记数法表示为( )
| A. | 69.6×104 | B. | 6.96×105 | C. | 6.96×106 | D. | 0.696×106 |
2.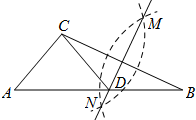 如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
 如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )| A. | ∠CAD=40° | B. | ∠ACD=70° | C. | 点D为△ABC的外心 | D. | ∠ACB=90° |
20. 如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
 如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
如图,∠ACD=120°,∠B=20°,则∠A的度数是( )| A. | 120° | B. | 90° | C. | 100° | D. | 30° |
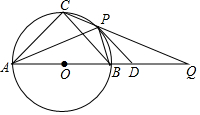 如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为弧$\widehat{BC}$上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论正确的是②③④.(写出所有正确结论的序号)
如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为弧$\widehat{BC}$上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论正确的是②③④.(写出所有正确结论的序号) 如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AB=16cm,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向B点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AB=16cm,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向B点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.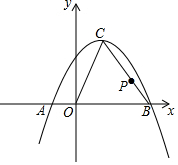 已知:如图,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).
已知:如图,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).