题目内容
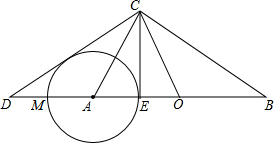
15. 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
(3)在(2)的条件下,直接写出tan∠CAB的值.
分析 (1)连接OD欲证明DE是⊙O的切线,只要证明∠ODE=90°即可.
(2)连接CD,首先求出AD,由△ACD∽△ADE,得到$\frac{AD}{AE}$=$\frac{AC}{DA}$,即可求出AC解决问题.
(3)作OF⊥MN于F,则四边形ODEF是矩形,根据tan∠CAB=$\frac{OF}{AF}$,求出AF即可解决问题.
解答 (1)证明:连接OD.
∵OA=OD
∴∠OAD=∠ODA
∵∠OAD=∠DAE
∴∠ODA∠DAE.
∴DO∥MN,
∵DE⊥MN,
∴∠ODE=∠DEM=90°
即OD⊥DE,
∵D在⊙O上
∴DE是⊙O的切线.
(2)解:连接CD
∵∠AED=90°,DE=6,AE=3,
∴AD=$\sqrt{D{E}^{2}+A{E}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∵AC是⊙O的直径,
∴∠ADC=∠AED=90°,
∵∠CAD=∠DAE,
∴△ACD∽△ADE,
∴$\frac{AD}{AE}$=$\frac{AC}{DA}$,
∴$\frac{3\sqrt{5}}{3}$=$\frac{AC}{3\sqrt{5}}$,
∴AC=15,
∴⊙O的半径是7.5cm.
(3)解:作OF⊥MN于F,则四边形ODEF是矩形,OF=AD=6,
∴AF=$\sqrt{O{A}^{2}-O{F}^{2}}$=$\sqrt{7.{5}^{2}-{6}^{2}}$=4.5,
∴tan∠CAB=$\frac{OF}{AF}$=$\frac{6}{4.5}$=$\frac{4}{3}$.
点评 本题考查圆综合题、切线的判定、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,灵活应用相似三角形性质解决问题,属于中考常考题型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在⊙O中,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
如图,在⊙O中,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
 如图,在△ABC与△OCD中,∠ACB=∠DCO=90°,O为AB的中点.
如图,在△ABC与△OCD中,∠ACB=∠DCO=90°,O为AB的中点.