题目内容
如图，一块四边形ABCD，已知AD=4m，CD=3m，∠ADC=90°，AB=13m，BC=12m，则这块地的面积为_______㎡．
- A.24
- B.30
- C.48
- D.60
A
分析：连接AC，由AD=4m，CD=3m，∠ADC=90°利用勾股定理可求出AC的长，在根据AB=13m，BC=12m，利用勾股定理的逆定理可证△ACB为直角三角形，然后即可求出这块地的面积．
解答：连接AC，
∵AD=4m，CD=3m，∠ADC=90°，
∴AC=
=
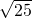=5，
∵AB=13m，BC=12m，
∴AB2=BC2+CD2，即△ABC为直角三角形，
∴这块地的面积为S△ABC-S△ACD=
AC•BC-AD•CD=×5×12-×3×4=24．
故选A．
点评：此题主要考查勾股定理和勾股定理的逆定理等知识点，难度不大，解答此题的关键是连接AC，求出三角形ABC的面积，再减去三角形ACD的面积即可．
分析：连接AC，由AD=4m，CD=3m，∠ADC=90°利用勾股定理可求出AC的长，在根据AB=13m，BC=12m，利用勾股定理的逆定理可证△ACB为直角三角形，然后即可求出这块地的面积．
解答：连接AC，
∵AD=4m，CD=3m，∠ADC=90°，
∴AC=
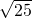==5，∵AB=13m，BC=12m，
∴AB2=BC2+CD2，即△ABC为直角三角形，
∴这块地的面积为S△ABC-S△ACD=
AC•BC-AD•CD=×5×12-×3×4=24．故选A．
点评：此题主要考查勾股定理和勾股定理的逆定理等知识点，难度不大，解答此题的关键是连接AC，求出三角形ABC的面积，再减去三角形ACD的面积即可．
练习册系列答案
阅读快车系列答案
相关题目
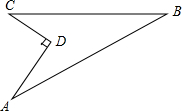如图，一块四边形ABCD，已知AD=4m，CD=3m，∠ADC=90°，AB=13m，BC=12m，则这块地的面积为（ ）㎡．| A、24 | B、30 | C、48 | D、60 |
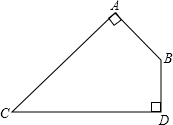如图，一块四边形土地，其中∠ABD=120°，AB⊥AC，BD⊥CD，AB=30
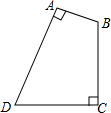如图，一块四边形土地，其中，∠A=∠C=90°，∠B=120°，AB=
某校学习小组到田间进行实践活动，如图是一块四边形稻田ABCD，小组同学测得以下数据：CD=AD=2m，∠D=60°，AB=BC=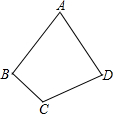
如图是一块四边形的薄钢板，∠A=60°，∠C=120°，AB=AD．