题目内容
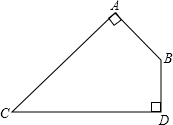 如图,一块四边形土地,其中∠ABD=120°,AB⊥AC,BD⊥CD,AB=30
如图,一块四边形土地,其中∠ABD=120°,AB⊥AC,BD⊥CD,AB=30| 3 |
| 3 |
分析:延长CA、DB交于点P,在Rt△CDP中根据三角函数可以求出PD,在Rt△PAB中可以求出PA,四边形的面积S四边形ACDB=S△CDP-S△ABP,就可以求得.
解答:解:延长CA、DB交于点P
∵∠ABD=120°,AB⊥AC,BD⊥CD.
∴∠ACD=60°,∠ABP=60°
在Rt△CDP中,
=tan∠ACD.
∴PD=CD•tan∠ACD=50
•
=150
在Rt△PAB中,
=tan∠PBA.
∴PA=AB•tan∠PBA=30
•
=90
∴S四边形ACDB=S△CDP-S△ABP
=
×50
×150-
×30
×90
=2400
答:这块土地的面积为2400
m2.

∵∠ABD=120°,AB⊥AC,BD⊥CD.
∴∠ACD=60°,∠ABP=60°
在Rt△CDP中,
| PD |
| CD |
∴PD=CD•tan∠ACD=50
| 3 |
| 3 |
在Rt△PAB中,
| PA |
| AB |
∴PA=AB•tan∠PBA=30
| 3 |
| 3 |
∴S四边形ACDB=S△CDP-S△ABP
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
=2400
| 3 |
答:这块土地的面积为2400
| 3 |
点评:本题主要考查了三角函数的定义,以及不规则图形可以看成一些易求面积的图形的和或差来计算.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
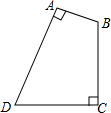 如图,一块四边形土地,其中,∠A=∠C=90°,∠B=120°,AB=
如图,一块四边形土地,其中,∠A=∠C=90°,∠B=120°,AB=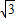 m,CD=50
m,CD=50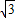 m,求这块土地的面积.
m,求这块土地的面积.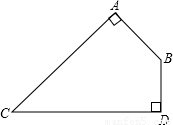
 m,CD=50
m,CD=50 m,求这块土地的面积.
m,求这块土地的面积.
 m,CD=50
m,CD=50 m,求这块土地的面积.
m,求这块土地的面积.