题目内容
6.一条直线上有8个点,则以这8个点为端点的线段共有( )| A. | 7条 | B. | 14条 | C. | 16条 | D. | 28条 |
分析 根据定义,线段是两端点及这两点之间的部分,找出线段再计算个数即可.
解答 解:$\frac{1}{2}$×8×(8-1)
=$\frac{1}{2}$×8×7
=28(条).
答:以这8个点为端点的线段共有28条.
故选:D.
点评 本题考查了线段条数的确定,对于端点个数比较少的情况,可以直接查出然后计算个数,对于比较多的情况可以利用公式$\frac{1}{2}$nn(n-1)(n是所有端点的个数)求解.

练习册系列答案
相关题目
17.$\sqrt{a^2}$=( )
| A. | a | B. | -a | C. | ${({\sqrt{a}})^2}$ | D. | |a| |
14.下列说法正确的是( )
| A. | 单项式x没有系数 | B. | mn2与-$\frac{1}{2}$n2m是同类项 | ||
| C. | 3x3y的次数是3 | D. | 多项式3x-1的项是3x和1 |
1. 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究.探究过程如下,请补充完整.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究.探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:
其中,m=0,n=0.
(2)根据表格数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
(3)观察函数图象,写出两条函数的性质:①函数图象是轴对称图形,关于y轴对称;②当x>1时,y随x的增大而增大.
(4)进一步探究函数图象发现:
①函数图象与x轴有3个交点,所以对应的方程x2-2|x|=0有3个实数根;
②方程x2-2|x|=2有2个实数根.
 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究.探究过程如下,请补充完整.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究.探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:
| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | 3 | $\frac{5}{4}$ | m | -1 | 0 | -1 | n | $\frac{5}{4}$ | 3 | … |
(2)根据表格数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
(3)观察函数图象,写出两条函数的性质:①函数图象是轴对称图形,关于y轴对称;②当x>1时,y随x的增大而增大.
(4)进一步探究函数图象发现:
①函数图象与x轴有3个交点,所以对应的方程x2-2|x|=0有3个实数根;
②方程x2-2|x|=2有2个实数根.
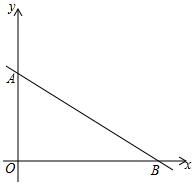 如图,一次函数y=-$\frac{3}{4}$x+6的图象分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.
如图,一次函数y=-$\frac{3}{4}$x+6的图象分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.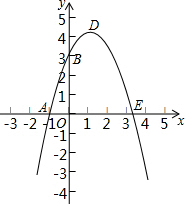 已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.
已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.