题目内容
9. 如图,长方形ABCD的长是n厘米.宽是m厘米,以AD为直径作扇形,以BC为半径作扇形.
如图,长方形ABCD的长是n厘米.宽是m厘米,以AD为直径作扇形,以BC为半径作扇形.(1)用代数式表示阴影部分的面积S;
(2)求当n=4厘米,m=2厘米,π≈3时,求出阴影郁分的面积S.
分析 (1)由已知图可知,阴影部分的面积为长方形的面积减去两个扇形的面积(一个直径为m的半圆,一个半径为m的$\frac{1}{4}$圆);
(2)把数值代入(1)中的式子,再进行计算,即可得出答案.
解答 解:(1)阴影部分的面积S=mn-$\frac{1}{2}$π×($\frac{m}{2}$)2-$\frac{1}{4}$πm2=mn-$\frac{3}{8}$πm2;
(2)当n=4厘米,m=2厘米,π≈3时,
阴影部分的面积S=4×2-$\frac{3}{8}$×3×22=$\frac{7}{2}$.
点评 此题考查列代数式以及代数式求值,掌握组合面积的计算方法是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
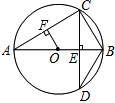 如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F,
如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F, 如图,在⊙O中,AB=2CD,求证:$\widehat{AB}$>2$\widehat{CD}$.
如图,在⊙O中,AB=2CD,求证:$\widehat{AB}$>2$\widehat{CD}$.