题目内容
19.一个长方体容器的容积为30m3,开始用一根细水管向容器内注水,水面高度到达容器高度一半后,改用一根注水速度为细水管注水速度2倍的水管注水,向容器中注满水全过程共用60min,求两根水管各自的注水速度.分析 设第一根细水管进水速度为xm3/min,则第二根水管进水速度为2xm3/min,一个长方体容器的容积为30m3,开始用一根细水管向容器内注水,水面高度到达容器高度一半后,改用一根注水速度Wie细水管注水速度2倍的水管注水,向容器中注满水全过程共用60min可列方程求解.
解答 解:设第一根细水管进水速度为xm3/min,则第二根水管进水速度为2xm3/min,根据题意得
$\frac{15}{x}$+$\frac{15}{2x}$=60,
解得:x=$\frac{3}{8}$,
经检验x=$\frac{3}{8}$是原方程的解.
答:第一根细水管进水速度为$\frac{3}{8}$m3/min,则第二根水管进水速度为$\frac{3}{4}$m3/min.
点评 本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.在Rt△ABC中,∠C=90°,若tan$\frac{B}{2}$=$\frac{\sqrt{3}}{3}$,则sinB的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
 如图,长方形ABCD的长是n厘米.宽是m厘米,以AD为直径作扇形,以BC为半径作扇形.
如图,长方形ABCD的长是n厘米.宽是m厘米,以AD为直径作扇形,以BC为半径作扇形.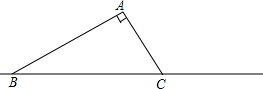 已知,如图,在△ABC中,AC=3厘米,BC=6厘米,∠C=60°,求:
已知,如图,在△ABC中,AC=3厘米,BC=6厘米,∠C=60°,求: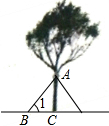 在台风来临之前,有关部门用钢管加固树木(如图).已知固定点A离地面的高度AC为3m,钢管脚的支撑点B离树干底部C点的距离为2m.求钢管与地面所成角∠1的大小(精确到1″).
在台风来临之前,有关部门用钢管加固树木(如图).已知固定点A离地面的高度AC为3m,钢管脚的支撑点B离树干底部C点的距离为2m.求钢管与地面所成角∠1的大小(精确到1″).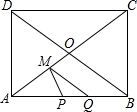 如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=8cm,BC=6cm,定长为2cm的动线段PQ在边AB上,端点P从点A开始沿边AB以1cm/s的速度向点B运动,当端点Q到达点B时运动停止,过点Q作QM∥BD交AC于点M(当点Q与点B重合时,QM与BO重合),连接PM.设线段PQ的运动时间为t(s)(t≥0).
如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=8cm,BC=6cm,定长为2cm的动线段PQ在边AB上,端点P从点A开始沿边AB以1cm/s的速度向点B运动,当端点Q到达点B时运动停止,过点Q作QM∥BD交AC于点M(当点Q与点B重合时,QM与BO重合),连接PM.设线段PQ的运动时间为t(s)(t≥0).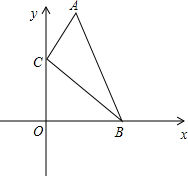 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.
如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.